Giải câu 4 bài hai dạng phương trình quy về phương trình bậc hai
Bài tập 4. Một người đứng ở điểm $A$ trên một bờ sông rộng $300 \mathrm{~m}$, chèo thuyền đến vị trí $D$, sau đó chạy bộ đến vị trí $B$ cách $C$ một khoảng $800 \mathrm{~m}$ (Hình 34). Vận tốc chèo thuyền là $6 \mathrm{~km} / \mathrm{h}$, vận tốc chạy bộ là $10 \mathrm{~km} / \mathrm{h}$ và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí $C$ đến $D$, biết tổng thời gian người đó chèo thuyền và chạy bộ từ $A$ đến $B$ (qua $D$ ) là 7,2 phút.
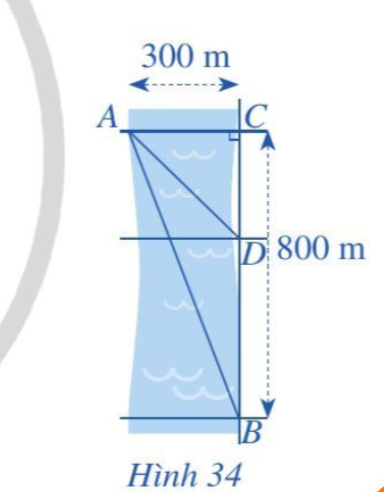
Đổi $300 \mathrm{~m}=0,3 \mathrm{~km}$, $800 \mathrm{~m}=0,8 \mathrm{~km}$; $7,2 \mathrm{~phút} =0,12(h)$
Gọi khoảng cách từ $C$ đến $D$ là $x$ (km) $(0<x<0,8)$
Khi đó, $DB=0,8-x$ (km)
Theo định lý Py-ta-go ta có: $AD=\sqrt{AC^{2}+CD^{2}}=\sqrt{0,3^{2}+x^{2}}(\mathrm{~km})$
Thời gian đi từ $\mathrm{A}$ đến $\mathrm{D}$ là: $\frac{\sqrt{0,3^{2}+x^{2}}}{6}(h)$
Thời gian đi từ $\mathrm{D}$ đến $\mathrm{B}$ là: $\frac{0,8-x}{10}(h)$
Theo bài ra ta có phương trình:$\frac{\sqrt{0,3^{2}+x^{2}}}{6}+\frac{0,8-x}{10}=0,12$
$\Leftrightarrow \sqrt{0,3^{2}+x^{2}} .5+(0,8-x).3=3,6$
$\Leftrightarrow 5. \sqrt{0,3^{2}+x^{2}}=3 x+1,2$
Ta có $3x+1,2 \geq 0 \Leftrightarrow x \geq -0,4$ (luôn đúng)
Bình phương hai vế ta được $25.(0,3^{2}+x^{2})=9x^2+7,2x+1,44$
$\Leftrightarrow 16x^2-7,2x+0,81=0 $
$\Leftrightarrow x=0,225$
Vậy khoảng cách từ $C$ đến $D$ là $225 \mathrm{~m}$.

Bình luận