Giải bài tập 7 trang 32 chuyên đề toán 10 chân trời sáng tạo

a, T1 là tổng tiền vốn và lãi của người đó có trong ngân hàng tại thời điểm ngay sau khi gửi vào khoản thứ 2: T1 = (a + ar) + a = a(1 + r) + a = a[(1 + r) + 1].

T2 là tổng tiền vốn và lãi của người đó có trong ngân hàng tại thời điểm ngay sau khi gửi vào khoản thứ 3:

 T2 = T1 + T1 . r + a

 T3 là tổng tiền vốn và lãi của người đó có trong ngân hàng tại thời điểm ngay sau khi gửi vào khoản thứ 4:

b, Từ câu a) ta có thể dự đoán:

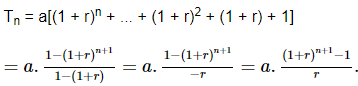
 Ta chứng minh bằng quy nạp toán học.

Với n = 1 ta có:

Như vậy khẳng định đúng cho trường hợp n = 1.

 Giả sử khẳng định đúng với n = k ≥ 1, tức là ta có

 Ta sẽ chứng minh rằng khẳng định cũng đủng với n = k + 1, nghĩa là ta sẽ chứng minh:

 Thật vậy,

T(k + 1) = Tk + Tk . r + a

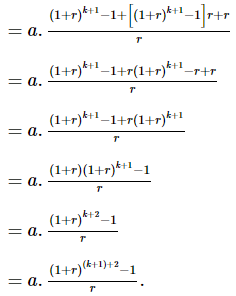
Vậy khẳng định đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, khẳng định đúng với mọi số tự nhiên n ≥ 1.

Vậy với mọi số tự nhiên n ≥ 1.