Giải bài tập 1 trang 32 chuyên đề toán 10 chân trời sáng tạo

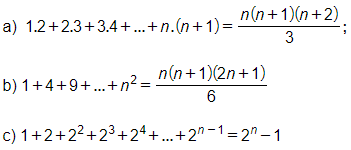
a, )  Với n = 1, ta có 

Do đó đẳng thức đúng với n = 1.

Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có:

 Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

Sử dụng giả thiết quy nạp, ta có:

 Vậy đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.

b, Với n = 1, ta có 

Do đó đẳng thức đúng với n = 1.

Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có:

Sử dụng giả thiết quy nạp, ta có:

 Vậy đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.

c, Với n = 1, ta có 2^(1 – 1) = 2^0 = 1 = 21 – 1.

Do đó đẳng thức đúng với n = 1.

Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có:

 Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

 Sử dụng giả thiết quy nạp, ta có:

 Vậy đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.