Giải Bài tập 5 trang 54 sgk Toán 8 tập 2 Chân trời

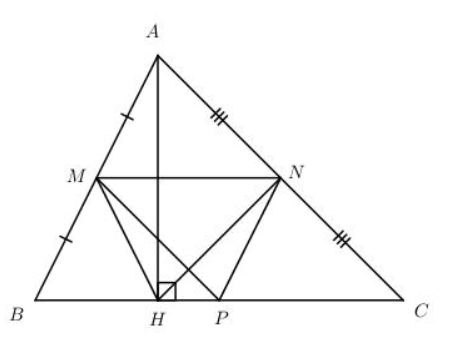
Xét tam giác ABC ta có:

M là trung điểm của AB (gt) ;

N là trung điểm của AC (gt) ;

⇒ MN là đường trung bình của tam giác ABC ⇒MN//BC

⇒ Tứ giác MNPH là hình thang.

Xét tam giác ABC ta có 

M là trung điểm của AB (gt) ;

P là trung điểm của BC

⇒MP là đường trung bình của tam giác ABC ⇒MP=$\frac{1}{2}$AC

ΔACH vuông tại H có HN là trung tuyến (N là trung điểm của AC)⇒NH=$\frac{1}{2}$AC. Mà MP=$\frac{1}{2}$AC(cmt)

⇒NH=MP

Hình thang MNPH (MN//PH) có MP=NH nên là hình thang cân.