Giải bài tập 3.14 trang 37 SBT toán 8 tập 1 kết nối:

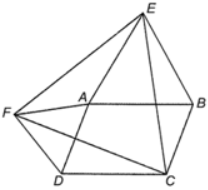
Do ABCD là hình bình hành nên AB // CD 

Gọi $\widehat{BAD}=\alpha $

Vì AB // CD nên ta có $\widehat{BAD}+\widehat{ADC}=180^{o}$

=> $\widehat{ADC}=180^{o}-\alpha $

$\widehat{CDF}=\widehat{ADC}+\widehat{ADF}=180^{o}-\alpha +60^{o}=240^{o}-\alpha$

Ta có: $\widehat{EAF}+\widehat{FAD}+\widehat{DAB}+\widehat{BAE}=360^{o}$

=> $\widehat{EAF}=360^{o}-\widehat{FAD}-\widehat{DAB}-\widehat{BAE}$

Mà $\widehat{FAD}=\widehat{BAE}=60^{o}$ (do ∆AFD và ∆ABE đều)

=> $\widehat{EAF}=360^{o}-60^{o}-60^{o}-\alpha $ = $240^{o}-\alpha$

=> $\widehat{CDF}=\widehat{EAF}$

Xét ∆AEF và ∆DCF có

AF = DF ( vì ∆ADF đều);

$\widehat{CDF}=\widehat{EAF}$ (chứng minh trên);

AE = DC (vì cùng bằng AB)

Do đó: ∆AEF =  ∆DCF (c.g.c)

Suy ra EF = CF (*)

$\widehat{CBE}=\widehat{ABC}+\widehat{ABE}=\widehat{ABC}+60^{o}$

Mà ABCD là hình bình hành nên $\widehat{ABC}=\widehat{ADC}=180^{o}-\alpha$

=> $\widehat{CBE}=180^{o}-\alpha+60^{o}$ = $240^{o}-\alpha$ mà $\widehat{CDF}= $240^{o}-\alpha$ (chứng minh trên)

=> $\widehat{CBE}=\widehat{CDF}$

Xét ΔBCE và ΔDFC có:

BE = CD (vì cùng bằng AB);

$\widehat{CBE}=\widehat{CDF}$ (chứng minh trên);

BC = DF (vì cùng bằng AD)

Do đó ∆BCE = ∆DFC (c.g.c)

Suy ra CE = CF (**)

Từ (*) và (**) suy ra: EF = CF = CE

Vậy ∆ECF là tam giác đều.