Giải bài 3 trang 75 toán 7 tập 2 chân trời sáng tạo

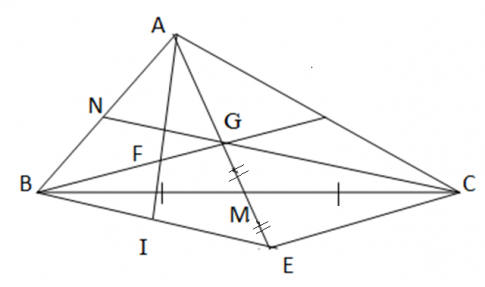
a) Xét  ∆BMG và  ∆CME ta có:

BM = CM (M là trung điểm của BC)

$\widehat{BMG}$  = $\widehat{CME}$ (hai góc đối đỉnh)

ME = MG (giả thiết)

=> ∆ BMG = ∆ CME (c.g.c)

=> $\widehat{GBM}$  = $\widehat{BCE}$;

Mà hai góc ở vị trị so le trong

=> GB // CE.

b) Xét tam giác ABC có AM và CN là hai đường trung tuyến cắt nhau tại G

=> G là trọng tâm của tam giác ABC

=> AG = 2GM

+ Ta có: GE = GM + EM

=> GE = 2GM (GM = EM)

=> AG = GE

=> G là trung điểm đoạn thẳng AE

=> BG là đường trung tuyến của tam giác ABM.

+ Xét tam giác ABM có: AI và BG là 2 đường trung tuyến

mà AI cắt BG tại F

=> F là trọng tâm của tam giác ABC

=> AF = 2FI.