Giải chi tiết bài 6.11 trang 70 sách toán 12 tập 2 kntt
Giải chi tiết bài 6.11 trang 70 sách toán 12 tập 2 kntt
Một bộ lọc được sử dụng để chặn thư rác trong các tài khoản thư điện tử. Tuy nhiên, vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất 0,95 và một thư đúng (không phải là thư rác) bị chặn với xác suất 0,01. Thống kê cho thấy tỉ lệ thư rác là 3%
a) Chọn ngẫu nhiên một thư bị chặn. Tính xác suất để đó là thư rác.
b) Chọn ngẫu nhiên một thư không bị chặn. Tính xác suất để đó là thư đúng.
c) Trong số các thư bị chặn, có bao nhiêu phần trăm là thư đúng? Trong số các thư không bị chặn, có bao nhiêu phần trăm là thư rác?
Gọi A là biến cố:”Thư bị chặn”
B là biến cố:”Thư đó là thư rác”
Vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất 0,95 và một thư đúng (không phải là thư rác) bị chặn với xác suất 0,01 nên:
và 
Tỉ lệ thư rác là 3% nên: 
a) Ta cần tính 
Theo công thức Bayes ta có:
Theo công thức xác suất toàn phần, ta có:
Hay 
Thay vào công thức ta có:
Vây xác suất để thư bị chặn là thư rác là 0,746
b) Ta cần tính 
Theo công thức Bayes ta có:
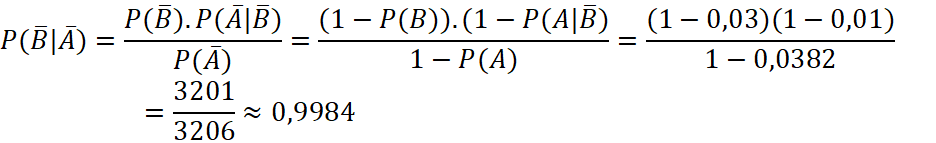
Vậy xác suất để thư không bị chặn là thư đúng là 0,9984
c)
- Ta cần tính
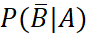
Vậy trong số các thư bị chặn, có 25,39% là thư đúng
- Ta cần tính
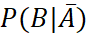
Vậy trong số các thư không bị chặn, có 0,156% là thư rác
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều
Trắc nghiệm 12 Kết nối tri thức
Trắc nghiệm 12 Chân trời sáng tạo
Trắc nghiệm 12 Cánh diều
Chuyên đề lớp 12
Bình luận