Câu hỏi tự luận mức độ nhận biết Toán 9 cd bài 1: Đường tròn. Vị trí tương đối của hai đường tròn
1. NHẬN BIẾT (5 câu)
Câu 1: Tìm số điểm chung của hai đường tròn (O) và (O’) trong mỗi trường hợp sau:

Câu 2: Cho hai đường tròn phân biệt (O; R) và (O’; R’) với R ≥ R’. Hãy so sánh OO’ với R + R’ và R – R’ trong mỗi trường hợp sau:
Trường hợp 1: (O; R) và (O’; R’) không có điểm chung (Hình 1).

Hình 1
Trường hợp 2: (O; R) và (O’; R’) chỉ có một điểm chung (Hình 2).
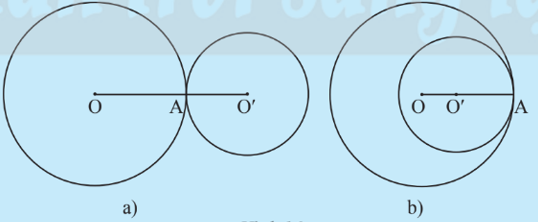
Hình 2
Câu 3: Cho hai đường tròn (O; 11,5 cm) và (O’; 6,5 cm). Biết rằng OO’ = 4 cm. Xét vị trí tương đối của hai đường tròn đó.
Câu 4: Xác định vị trí tương đối giữa hai đường tròn (I; R) và (J; R’) trong mỗi trường hợp sau:
a) IJ = 5; R = 3; R’ = 2 b) IJ = 4; R = 11; R’ = 7
c) IJ = 6; R = 9; R’ = 4 d) IJ = 10; R = 4; R’ = 1.
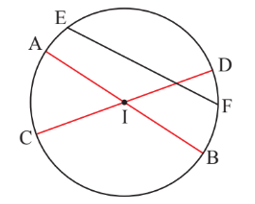
Câu 5: Cho đường tròn (I) có các dây cung AB, CD, EF. Cho biết AB và CD đi qua tâm I, EF không đi qua I (Hình vẽ). Hãy so sánh độ dài AB, CD, EF.
Câu 1:
Hình a): Hai đường tròn (O) và (O’) không có điểm chung.
Hình b): Hai đường tròn (O) và (O’) không có điểm chung.
Hình c): Hai đường tròn (O) và (O’) có một điểm chung là điểm M.
Hình d): Hai đường tròn (O) và (O’) có một điểm chung là điểm M.
Hình e): Hai đường tròn (O) và (O’) có hai điểm chung là điểm M và điểm N.
Câu 2:
– Trường hợp 1: (O; R) và (O’; R’) không có điểm chung (Hình 1).
Hình 1a): OO’ > R + R’; OO’ > R – R’;
Hình 1b): OO’ < R + R’; OO’ < R – R’.
– Trường hợp 2: (O; R) và (O’; R’) chỉ có một điểm chung (Hình 2).
Hình 2a): OO’ = R + R’; OO’ > R – R’;
Hình 2b): OO’ < R + R’; OO’ = R – R’.
Câu 3:
Ta thấy bán kính của hai đường tròn (O) và (O’) lần lượt là R = 11,5 cm và r = 6,5 cm.
Do R – r = 11,5 – 6,5 = 5 (cm) và 4 < 5 nên OO’ < R – r.
Vậy đường tròn (O; 11,5 cm) đựng đường tròn (O’; 6,5 cm).
Câu 4:
a) Ta có 5 = 3 + 2 nên IJ = R + R’, suy ra hai đường tròn (I; R) và (J; R’) tiếp xúc ngoài.
b) Ta có 4 = 11 – 7 nên IJ = R – R’, suy ra hai đường tròn (I; R) và (J; R’) tiếp xúc trong.
c) Ta có: 9 – 4 < 6 < 9 + 4 nên R – R’ < IJ < R + R’, suy ra hai đường tròn (I; R) và (J; R’) cắt nhau.
d) Ta có: 10 > 4 + 1 nên IJ > R + R’, suy ra hai đường tròn (I; R) và (J; R’) ở ngoài nhau.
Câu 5:
Trong đường tròn (I), AB và CD là đường kính đi qua tâm I, EF là dây cung không đi qua I.
Do đó AB = CD và EF < AB, EF < CD.
Vậy EF < AB = CD.
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận