CHƯƠNG III: GIỚI HẠN. HÀM SỐ LIÊN TỤC

BÀI 2: GIỚI HẠN CỦA HÀM SỐ

1. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM

a) Khi x càng gần đến 1 thì giá trị của hàm số càng gần đến 4 .

b) Điểm P càng gần đến điểm (0;4) trên trục tung khi điểm H càng gần về điểm (1;0) trên trục hoành.

*) Sử dụng giới hạn dãy số

Lấy dãy số (x$_{n}$) bất kì sao cho x$_{n}$≠1;x$_{n}$ =1. ta có

f(x$_{n}$)=$\frac{2_{n}^{2}-2}{x_{n}-1}$=$\frac{2(x_{n}+1)(x_{n}-1)}{x_{n}-1}$=2x$_{n}$+2.

Do đó, f(x$_{n}$) =(2x$_{n}$+2) =2x$_{n}$ +2 =2.1+2=4

Ta nói hàm số  y=fx có giới hạn là 4 khi x dần tới 1.

Kết luận:

Cho điểm x$_{0}$ thuộc khoảng K và hàm số y=f(x) xác định trên K hoặc K\{x$_{0}$}. Ta nói hàm số f(x) có giới hạn là số L khi x dần tới x$_{0}$ nếu với dãy số x$_{n}$ bất kì, x$_{n} \in $K\{x$_{0}$} và x$_{n} \rightarrow $x$_{0}$, thì f(x$_{n}$)$\rightarrow $L, kí hiệu

lim f(x)=L hay

x$\rightarrow $x$_{0}$
f(x)$\rightarrow $L khi x$\rightarrow $x$_{0}$. 

Ví dụ 1 (SGK -tr.72)

Nhận xét

lim  x$_{o}$ =x$_{o}$ ;

x$\rightarrow $x$_{0}$ 

lim c=c c là hằng số.

x$\rightarrow $x$_{0}$ 

Thực hành 1

a) Giả sử (x$_{n}$) là dãy số bất kì, thoả mãn x$_{n}$≠3 với mọi n và x$_{n} \rightarrow $3 khi n$\rightarrow $+∞. Ta có

lim(2$_{n}^{2}$-x$_{n}$)=2(limx$_{n}$)$^{2}$-limx$_{n}$=2⋅3$^{2}$-3=15. 

Vậy     lim (2x$^{2}$-x)=15

          x$\rightarrow $3  .

b) Giả sử x$_{n}$ là dãy số bất kì, thoả mãn x$_{n}$≠-1 với mọi n và xn$\rightarrow $-1 khi n$\rightarrow $+∞. Ta có

lim$\frac{x_{n}^{2}+2x_{n}+1}{x_{n}+1}$=lim$\frac{(x_{n}+1)^{2}}{x_{n}+1}$=lim(x$_{n}$+1)=limx$_{n}$+1=-1+1=0.

Vậy  lim $\frac{x^{2}+2x+1}{x+1}$=0.

        x$\rightarrow $-1 

2. CÁC PHÉP TOÁN VỀ GIỚI HẠN HỮU HẠN CỦA HÀM SỐ

HĐKP 2

a) Ta có lim[[f(x$_{n}$)+g(x$_{n}$)]=lim(2x$_{n}$+$\frac{x_{n}}{x_{n}+1}$)

=2limx$_{n}$+limxnxn+1=2⋅1+$\frac{1}{1+1}$=$\frac{5}{2}$.

b) Vì lim[f(x$_{n}$)+g(x$_{n}$)]=$\frac{5}{2}$

nên x$\rightarrow $1 [f(x)+g(x)]=$\frac{5}{2}$.

Ta có: limf(x$_{n}$)=lim(2x$_{n}$)=2lim(x$_{n}$)=2⋅1=2

f(x)=2;  

limg(x$_{n}$)=lim$\frac{x_{n}}{x_{n}+1}$=$\frac{limx_{n}}{limx_{n}+1}$=$\frac{1}{1+1}$=$\frac{1}{2}$

=> lim g(x)=$\frac{1}{2}$.

      x$\rightarrow $1 

Do đó   lim f(x)+x$\rightarrow $1 g(x)=2+$\frac{1}{2}$=$\frac{5}{2}$.

             x$\rightarrow $1 

Từ (1) và (2) suy ra 

lim[f(x)+g(x)]=lim f(x) + lim g(x).

x$\rightarrow $1               x$\rightarrow $1         x$\rightarrow $1 

Kết luận

+ Cho  lim f(x)=L và lim  g(x)=M. Khi đó

            x$\rightarrow $x$_{0}$             x$\rightarrow $x$_{0}$

lim [f(x)+g(x)]=L+M;lim[f(x)-g(x)]=L-M;lim [f(x)⋅g(x)]=L⋅M;lim f(x)g(x)=LM, nếu M≠0.

x$\rightarrow $x$_{0}$                         x$\rightarrow $x$_{0}$                  x$\rightarrow $x$_{0}$                 x$\rightarrow $x$_{0}$ 

+ Nếu f(x)≥0 và   lim  f(x)=L

                            x$\rightarrow $x$_{0}$

thì L≥0 và lim $\sqrt{f(x)}$=$\sqrt{L}$

                 x$\rightarrow $x$_{0}$

(Dấu của f(x) được xét trên khoảng tìm giới hạn, x≠x$_{0}$)

Nhận xét:

a) lim x$^{k}$=x$_{0}^{k}$, k là số nguyên dương;

     x$\rightarrow $x$_{0}$

b) lim [cf(x)]=c   lim f(x) (c∈R, nếu tồn tại limf(x)∈R)

     x$\rightarrow $x$_{0}$        x$\rightarrow $x$_{0}$                            x$\rightarrow $x$_{0}$

Ví dụ 2 (SGK -tr.73)

Ví dụ 3 (SGK -tr.73)

Thực hành 2

a) lim (x$^{2}$+5x-2)

     x$\rightarrow $-2 

=lim x$^{2}$ +5lim x - lim 2

   x$\rightarrow $-2    x$\rightarrow $-2     x$\rightarrow $-2 

=(-2)$^{2}$+5⋅(-2)-2=4-10-2=-8.

b)  lim $\frac{x^{2}-1}{x-1}$= lim  $\frac{(x-1)(x+1)}{x-1}$= lim (x+1)

     x$\rightarrow $1             x$\rightarrow $1        x$\rightarrow $1 

= lim  x+1=1+1=2.

    x$\rightarrow $1

3. GIỚI HẠN MỘT PHÍA

HĐKP 3:

a) Khi x$_{n}$∈(1;2,5) thì f(x$_{n}$)=7 nên limf(x$_{n}$)=7.

b) Khi x$_{n}$'∈(0;1) thì f(x$_{n}$)'=6 nên limf(x$_{n}$)'=6.

c) Ta thấy, mặc dù limx$_{n}$=limx$_{n}$'=1 nhưng limf(x$_{n}$)$\neq $limf(x$_{n}$)'. 

Kết luận

- Cho hàm số y=f(x) xác định trên khoảng (x$_{0}$;b). Ta nói y=f(x) có giới hạn bên phải là số L khi x$\rightarrow $x$_{0}$ nếu với dãy số xn bất kì thoả mãn x$_{0}$<x$_{n}$<b và x$_{n} \rightarrow $x$_{0}$, thì f( x$_{n}$)$\rightarrow $L, kí hiệu lim f(x) = L

                                                         x$\rightarrow $x$_{0}^{+}$.

- Cho hàm số y=f(x) xác định trên khoảng (a;x$_{0}$). Ta nói y=f(x) có giới hạn bên trái là số L khi x$\rightarrow $x$_{0}$ nếu với dãy số x$_{n}$ bất kì thoả mãn a<x$_{n}$<x$_{0}$ và x$_{n} \rightarrow $x$_{0}$, thì f(x$_{n}$)$\rightarrow $L, kí hiệu f(x) = L

                                                        x$\rightarrow $x$_{0}^{-}$.

Chú ý:

a) 

f(x) =L và f(x) =L khi và chỉ khi f(x) =L

Nếu f(x) =L$\neq $f(x) =L thì không tồn tại f(x) .

b) Các phép toán về giới hạn hữu hạn của hàm số vẫn đúng khi ta thay x$\rightarrow $x$_{0}$ bằng x$\rightarrow $x$_{0}^{+}$ hoặc x$\rightarrow $x$_{0}^{-}$.

Ví dụ 4 (SGK -tr.74)

Thực hành 3

Cách 1: Sử dụng dãy số như định nghĩa.

Cách 2: (Sử dụng biểu thức xác định hàm số trên từng khoảng)

Với x<-1,f(x)=1-2x nên 

lim f(x)=lim  (1-2x)=1-2.(-1)=3.

x$\rightarrow $x$_{-1}^{-}$.    x$\rightarrow $x$_{-1}^{-}$

Với x>-1,f(x)=x$^{2}$+2 nên

lim  f(x)= lim x$^{2}$+2=(-1)$^{2}$+2=3.

x$\rightarrow $x$_{-1}^{+}$    x$\rightarrow $x$_{-1}^{+}$

Do lim f(x)= lim f(x)=3 nên x→-1 f(x)=3.

     x$\rightarrow $x$_{-1}^{+}$    x$\rightarrow $x$_{-1}^{-}$

4. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC

HĐKP 4

a) 

Giá trị của f(x) dần về 0 khi x dần tới +∞.

b) 

Giá trị của f(x) dần về 0 khi x dần tới -∞.

*) Sử dụng giới hạn dãy số

Xét hàm số f(x)=$\frac{1}{x}$. Lấy dãy số xn bất kì sao cho x$_{n}$≠0 và x$_{n}$ =+∞. Khi đó

f(x$_{n}$) =$\frac{1}{x_{n}}$ =0

Kết luận

- Cho hàm số y=f(x) xác định trên khoảng (a;+∞). Ta nói hàm số f(x) có giới hạn hữu hạn là số L khi x$\rightarrow $+∞ nếu với dãy số x$_{n}$ bất kì, x$_{n}$> a và x$_{n} \rightarrow $+∞, ta có f(x$_{n}$)$\rightarrow $L, 

kí hiệu lim f(x)=L hay f(x)$\rightarrow $L khi x$\rightarrow $+∞.

             x$\rightarrow $+∞

- Cho hàm số y=f(x) xác định trên khoảng (-∞;a). Ta nói hàm số f(x) có giới hạn là số L khi x$\rightarrow $-∞ nếu với dãy số x$_{n}$ bất kì, x$_{n}$<b và x$_{n} \rightarrow $-∞, ta có f(x$_{n}$)$\rightarrow $L,

kí hiệu lim f(x)=L hay f(x)$\rightarrow $L khi x$\rightarrow $-∞.

            x$\rightarrow $-∞ 

Ví dụ 5 (SGK -tr.76)

Chú ý

- Với c là hằng số, k là một số nguyên dương ta có:

lim c=c;  lim $\frac{1}{x^{k}}$=0.

x$\rightarrow $±∞     x$\rightarrow $±∞ 

- Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.

Ví dụ 6 (SGK -tr.76)

Thực hành 4

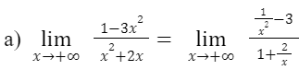
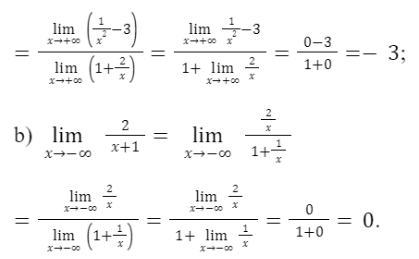
Vận dụng 1

a) Khối lượng muối có trong hồ là 200.10=2000( kg).

Sau t phút, lượng nước trong hồ là 200+2t (m$^{3}$).

Nồng độ muối tại thời điểm t phút kể từ khi bơm là C(t)=$\frac{2000}{200+2t}$ (kg/m$^{3}$).

b)

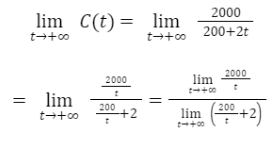
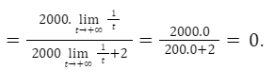
Điều này có nghĩa là khi t càng lớn thì nồng độ muối càng dần về 0 , tức đến một lúc nào đó nồng độ muối trong hồ không còn đáng kể và nước trong hồ gần như là nước ngọt.

5. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ TẠI MỘT ĐIỂM

HĐKP 5

a) 

Giá trị của f(x) trở nên rất lớn khi x dần tới 1 phía bên phải.

b) 

Giá trị của f(x) trở nên rất bé (giá trị của -f(x) trở nên rất lớn) khi x dần tới 1 phía bên trái.

Kết luận

- Cho hàm số y=f(x) xác định trên khoảng (x$_{0}$;b). 

+ Ta nói hàm số f(x) có giới hạn bên phải là +∞ khi x$\rightarrow $x$_{0}$ về bên phải nếu với dãy số x$_{n}$ bất kì thoả mãn x$_{0}$<x$_{n}$<b,x$_{n} \rightarrow $x$_{0}$, thì f(x$_{n}$)$\rightarrow $+∞, kí hiệu f(x)  =+∞.

+ Ta nói hàm số f(x) có giới hạn bên phải là - khi x$\rightarrow $x$_{0}$ về bên phải nếu với dãy số x$_{n}$ bất kì thoả mãn x$_{0}$<x$_{n}$<b,x$_{n} \rightarrow $x$_{0}$, thì f(x$_{n}$)$\rightarrow $-∞, kí hiệu f(x)  =-∞.

Chú ý:

- Các giới hạn

lim f(x)=+∞, lim  f(x)=-∞, lim  f(x)=+∞, lim  f(x)=-∞, lim  f(x)=+∞, lim  f(x)=+∞  được định nghĩa 

x$\rightarrow x_{0}^{-}$            x$\rightarrow  x_{0}^{-}$         x$\rightarrow $+∞        x$\rightarrow $+∞      x$\rightarrow $-∞  x$\rightarrow $-∞ 

tương tự.

- Các giới hạn thường dùng

lim$\frac{1}{x-a}$=+∞; lim $\frac{1}{x-a}$=-∞ (a∈R)

x$\rightarrow $a$^{+}$ ,         x$\rightarrow $a$^{-}$ 

lim x$^{k}$=+∞, k là số nguyên dương;

x$\rightarrow $+∞

lim x$^{k}$=+∞, k là số nguyên dương chẵn;

x$\rightarrow $-∞

lim x$^{k}$=-∞, k là số nguyên dương lẻ.

x$\rightarrow $-∞

c) Các phép toán trên giới hạn hàm số chỉ áp dụng khi tất cả các hàm số được xét có giới hạn hữu hạn.

Với giới hạn vô cực, ta có 

lim f(x)=L≠0 và lim g(x)=+∞ (hoặc -∞ ). Khi đó lim  [fx.gx] tính theo quy tắc

x$\rightarrow  _{0}^{+}$               x$\rightarrow  _{0}^{+}$                                      x$\rightarrow  _{0}^{+}$ 

Các quy tắc trên vẫn đúng cho trường hợp: x$\rightarrow  x_{0}^{-}$  (hoặc+∞,-∞).

• Quy tắc tìm giới hạn của thương $\frac{f(x)}{g(x)}$

Ví dụ 7 (SGK -tr.78)

Thực hành 5

a) lim 2x=6 và lim $\frac{1}{x-3}$=-∞ 

     x$\rightarrow $3-            x$\rightarrow $3-  

nên  lim $\frac{2x}{x-3}$= lim (2x.$\frac{1}{x-3}$)=-∞;

        x$\rightarrow $3-          x$\rightarrow $3-  

b) lim (3-$\frac{1}{x}$)=3 và lim  x=+∞ 

     x$\rightarrow $+∞               x$\rightarrow $+∞

nên lim (3x-1)= lim [x(3-$\frac{1}{x}$)]=+∞.

       x$\rightarrow $+∞         x$\rightarrow $+∞ 

Vận dụng 2

Ta có S(x)=x.$\frac{1}{x^{2}}$=$\frac{1}{x}$.

lim S(x)=lim 1x=+∞; lim S(x)= lim $\frac{1}{x}$=0.

 x$\rightarrow  _{0}^{+}$             x$\rightarrow  _{0}^{+}$               x$\rightarrow $+∞     x$\rightarrow $+∞