Slide bài giảng Toán 12 cánh diều Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Tóm lược nội dung

BÀI 4: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

I. SƠ ĐỒ KHẢO SÁT HÀM SỐ

Hoạt động: Lập bảng biến thiên và vẽ đồ thị của hàm số .

Trả lời rút gọn:

1.  .
2. Sự biến thiên:

• Giới hạn tại vô cực: 

; ↔ ↔

1. Vẽ đồ thị hàm số

Luyện tập 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số .

Trả lời rút gọn:

1.  .
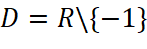2. Sự biến thiên:

• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

, . Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.

, . Do đó, đường thẳng là tiệm cận ngang của đồ thị hàm số.

• với .

Hàm số đồng biến trên mỗi khoảng và .

Hàm số không có cực trị.

1. Đồ thị

• Giao điểm của đồ thị với trục tung: .
• Giao điểm của đồ thị với trục hoành: .
• Đồ thị hàm số đi qua các điểm , , 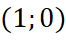và .
• Đồ thị hàm số nhận giao điểm của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

Vậy đồ thị hàm số được cho ở hình trên.

II. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ BẬC BA

Luyện tập 2: Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

1. ;
2. .

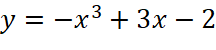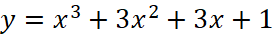Trả lời rút gọn:

1.  
2. .
3. Sự biến thiên:

• Giói hạn tại vô cực: , .
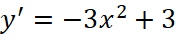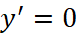• ; ↔ ↔ (thỏa mãn).

Hàm số đã cho đồng biến trên khoảng , nghịch biến trên mỗi khoản và .

Hàm số đạt cực đại tại , ; hàm số đạt cực tiểu tại , .

1. Đồ thị: 

• Giao điểm của đồ thị với trục tung: .
• Các giao điểm của đồ thị với trục hoành: và .
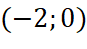• Đồ thị hàm số đi qua các điểm , , và .

Vậy đồ thị hàm số được cho như hình trên.

1.  
2.  .
3. Sự biến thiên:

• Giới hạn tại vô cực: , .
• ; với (Dấu xảy ra ↔ ).

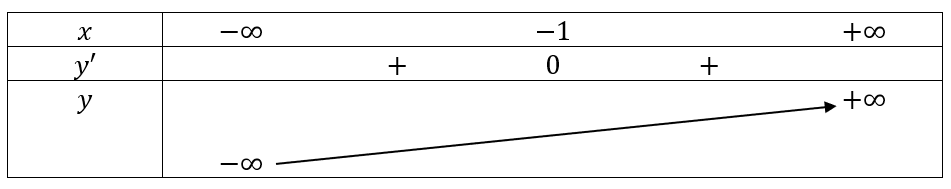
Hàm số đồng biến trên khoảng .

Hàm số không có cực trị.

1. Đồ thị:

• Giao điểm của đồ thị với trục tung: .
• Giao điểm của đồ thị với trục hoành: .
• Đồ thị hàm số đi qua các điểm , , .

Vậy đồ thị hàm số được cho như hình vẽ trên.

III. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA MỘT SỐ HÀM PHÂN THỨC HỮU TỈ

Luyện tập 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số .

Trả lời rút gọn:

1.  .
2. Sự biến thiên:

• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

, . Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.

, . Do đó, đường thẳng là tiệm cận ngang của đồ thị hàm số.

• với .

Hàm số đồng biến trên mỗi khoảng và .

Hàm số không có cực trị.

1. Đồ thị:

• Giao điểm của đồ thị với trục tung: .
• Giao điểm của đồ thị với trục hoành: .
• Đồ thị hàm số đi qua các điểm 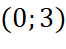, , và .
• Đồ thị hàm số nhận giao điểm của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

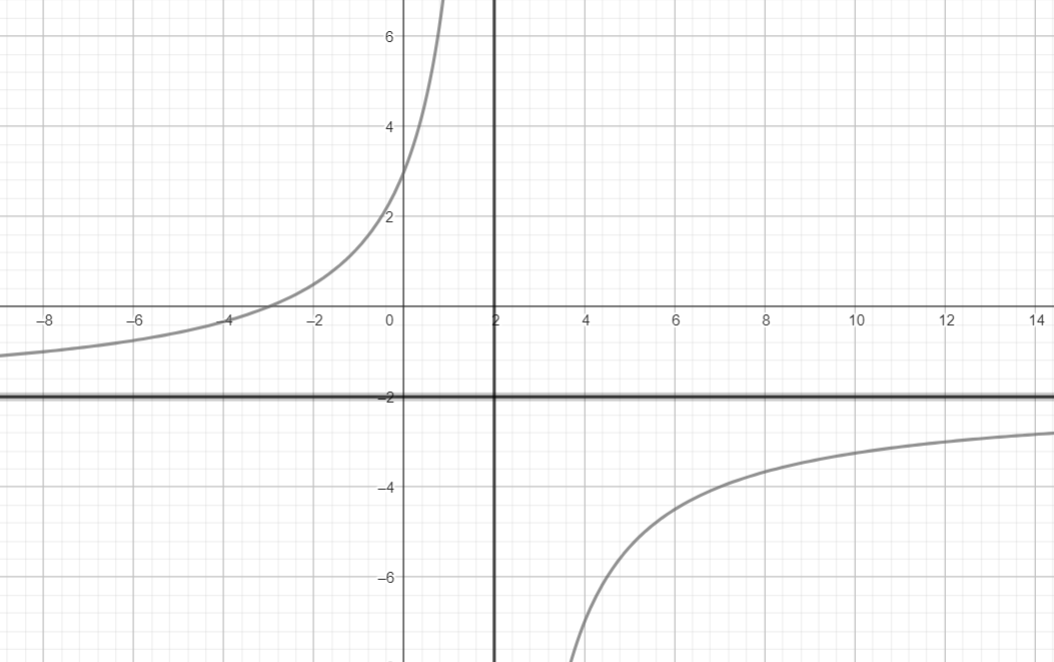
Vậy đồ thị hàm số được cho ở hình trên.

Luyện tập 4: Khảo sát sự biến thiên và vẽ đồ thị hàm số .

Trả lời rút gọn:

1. .
2. Sự biến thiên:

• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

, . Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.

, . Do đó, đường thẳng là tiệm cận ngang của đồ thị hàm số.

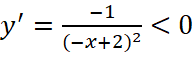• với .

Hàm số nghịch biến trên mỗi khoảng và .

Hàm số không có cực trị.

1. Đồ thị:

• Giao điểm của đồ thị với trục tung: .
• Giao điểm của đồ thị với trục hoành: .
• Đồ thị hàm số đi qua các điểm , , 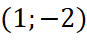và .
• Đồ thị hàm số nhận giao điểm 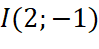của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

Vậy đồ thị hàm số được cho ở hình trên.

Luyện tập 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số .

Trả lời rút gọn:

1.  .
2. Sự biến thiên:

• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

, .

, . Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.

, . Do đó, đường thẳng là tiệm cận xiên của đồ thị hàm số.

• ; ↔ (thỏa mãn) hoặc (thỏa mãn)

Hàm số đồng biến trên mỗi khoảng và ; nghịch biến trên mỗi khoảng và .

Hàm số đạt cực đại tại , ; đạt cực tiểu tại , .

1. Đồ thị:

• Đồ thị đi qua gốc tọa độ .
• Đồ thị hàm số đi qua các điểm , , và và .
• Đồ thị hàm số nhận giao điểm của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

Vậy đồ thị hàm số được cho ở hình trên.

CÒN TIẾP…