Slide bài giảng Toán 12 cánh diều Bài 1: Vectơ và các phép toán vectơ trong không gian
Slide điện tử Bài 1: Vectơ và các phép toán vectơ trong không gian. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 12 Cánh diều sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 1: VECTO VÀ CÁC PHÉP TOÁN VECTO TRONG KHÔNG GIAN
I. KHÁI NIỆM VECTO TRONG KHÔNG GIAN
Hoạt động 1: Trong mặt phẳng, hãy nêu định nghĩa:
- Vecto, giá và độ dài của vecto, hai vecto cùng phương, hai vecto cùng hướng;
- Vecto-không;
- Hai vecto bằng nhau, hai vecto đối nhau.
Trả lời rút gọn:
- Vecto là một đoạn thẳng có hướng.
Giá của vecto là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.
Độ dài của vecto là khoảng cách giữa điểm đầu và điểm cuối của vecto đó.
Hai vecto được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
Nếu hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng. Hai vecto cùng hướng khi chúng có cùng chiều từ điểm đầu đến điểm cuối.
- Vecto-không là vecto có điểm đầu và điểm cuối trùng nhau, là
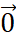 .
. - Hai vcto bằng nhau nếu chúng cùng hướng và cùng độ dài.
Vecto có cùng độ dài và ngược hướng với vecto ![]() , ký hiệu là
, ký hiệu là ![]() .
.
Hai vecto ![]() và
và ![]() được gọi là hai vecto đối nhau.
được gọi là hai vecto đối nhau.
Luyện tập 1: Cho hình hộp ![]() . Hãy chỉ ra ba vecto có điểm đầu và điểm cuối là các đỉnh của hình hộp sao cho mỗi vecto đó:
. Hãy chỉ ra ba vecto có điểm đầu và điểm cuối là các đỉnh của hình hộp sao cho mỗi vecto đó:
- Bằng vecto
 ;
; - Là vecto đối của vecto
 .
.
Trả lời rút gọn:
- Do các vecto
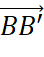 ,
,  ,
, 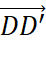 cùng hướng với vecto
cùng hướng với vecto 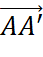 và
và 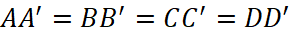 (tính chất hình hộp) nên
(tính chất hình hộp) nên  .
.
Vậy ba vecto ![]() ,
, ![]() ,
, ![]() có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vecto
có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vecto ![]() .
.
- Do các vecto
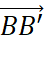 ,
,  ,
, 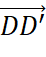 ngược hướng với vecto
ngược hướng với vecto  và
và 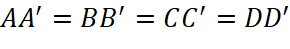 nên ba vecto
nên ba vecto 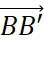 ,
,  ,
, 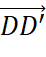 là ba vecto đối của vecto
là ba vecto đối của vecto  .
.
II. CÁC PHÉP TOÁN VECTO TRONG KHÔNG GIAN
Hoạt động 2: Trong không gian, cho hai vecto ![]() ,
, ![]() . Lấy một điểm
. Lấy một điểm ![]() tùy ý.
tùy ý.
- Vẽ
 ,
,  .
. - Tổng của hai vecto
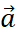 và
và 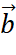 bằng vecto nào trong Hình 4?
bằng vecto nào trong Hình 4?
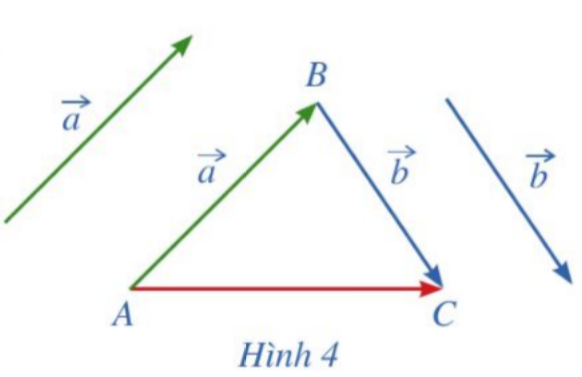
Trả lời rút gọn:
- Từ điểm
 , ta vec đường thẳng song song với giá của vecto
, ta vec đường thẳng song song với giá của vecto 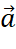 , trên đường thẳng này, ta lấy điểm
, trên đường thẳng này, ta lấy điểm  sao cho hai vecto
sao cho hai vecto 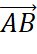 và
và 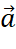 cùng hướng, đồng thời
cùng hướng, đồng thời 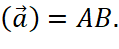
![]() . Tương tự ta vẽ vecto
. Tương tự ta vẽ vecto ![]() .
.
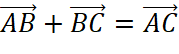 .
.
Vậy tổng của hai vecto ![]() và
và ![]() bằng vecto
bằng vecto ![]() .
.
Luyện tập 2: Cho tứ diện ![]() . Chứng minh rằng
. Chứng minh rằng ![]() .
.
Trả lời rút gọn:
![]() .
.
![]() .
.
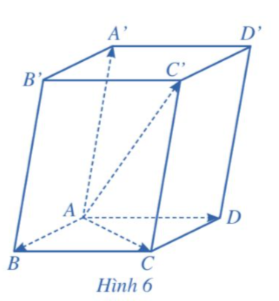
Hoạt động 3: Cho hình hộp ![]() (Hình 6). Tìm liên hệ giữa:
(Hình 6). Tìm liên hệ giữa: ![]() và
và ![]() ;
; ![]() và
và ![]() . Từ đó, hãy suy ra rằng:
. Từ đó, hãy suy ra rằng: ![]() .
.
Trả lời rút gọn:
Vì ![]() là hình hộp nên
là hình hộp nên ![]() và
và ![]() là các hình bình hành.
là các hình bình hành.
![]() là hình bình hành nên:
là hình bình hành nên: ![]() .
.
![]() là hình bình hành nên:
là hình bình hành nên: ![]() .
.
=> ![]() .
.
![]() .
.
Luyện tập 3: Cho hình hộp ![]() . Chứng minh rằng:
. Chứng minh rằng:
![]()
Trả lời rút gọn:
Vì ![]() là hình hộp nên ta có:
là hình hộp nên ta có: ![]() ,
, ![]() .
.
=> ![]() .
.
Hoạt động 4: Trong không gian, cho hai vecto ![]() ,
, ![]() . Lấy một điểm
. Lấy một điểm ![]() tùy ý.
tùy ý.
- Vẽ
 ,
, 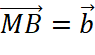 ,
,  .
. - Tổng của hai vecto
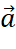 và
và  bằng vecto nào trong Hình 7?
bằng vecto nào trong Hình 7?
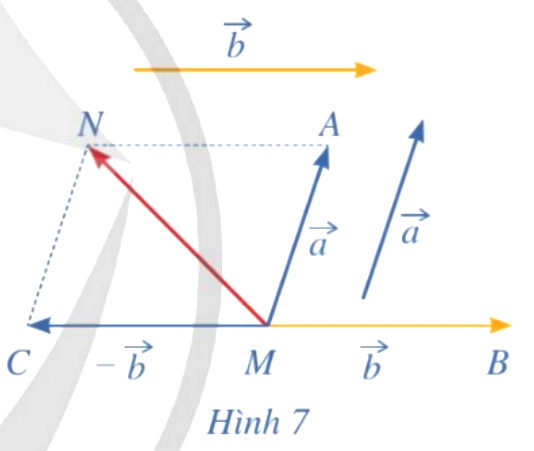
Trả lời rút gọn:
- Như Hình 7.
- Dựng hình bình hành
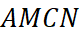 , khi đó ta có:
, khi đó ta có:
![]()
Vậy tổng của hai vecto ![]() và
và ![]() bằng vecto
bằng vecto ![]() .
.
Luyện tập 4: Cho hình hộp ![]() . Chứng minh rằng:
. Chứng minh rằng:
![]()
Trả lời rút gọn:
![]()
![]()
Hoạt động 5: Nêu định nghĩa của một số thực ![]() và vecto
và vecto ![]() trong mặt phẳng.
trong mặt phẳng.
Trả lời rút gọn:
Cho số thực ![]() và vecto
và vecto ![]() . Tích của một số
. Tích của một số ![]() với vecto
với vecto ![]() là một vecto, ký hiệu là
là một vecto, ký hiệu là ![]() , được xác định như sau:
, được xác định như sau:
Cùng hướng với vecto ![]() nếu
nếu ![]() , ngược hướng với vecto
, ngược hướng với vecto ![]() nếu
nếu ![]() ;
;
Có độ dài bằng ![]() .
.
Luyện tập 5: Cho tứ diện ![]() . Gọi
. Gọi ![]() ,
, ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() và
và ![]() ,
, ![]() là trung điểm
là trung điểm ![]() . Chứng minh rằng:
. Chứng minh rằng:
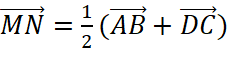 ;
; .
.
Trả lời rút gọn:
- Vì
 là trung điểm của
là trung điểm của  nên với điểm
nên với điểm  , ta có:
, ta có: 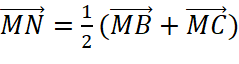 .
.
: ![]() ,
, ![]() .
.
Lại có ![]() là trung điểm của
là trung điểm của ![]() nên
nên ![]() .
.
![]()
![]() .
.
=> ![]() .
.
- Vì
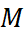 ,
,  lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 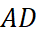 và
và  nên ta có:
nên ta có:
![]() ,
, ![]() .
.
![]()
Vì ![]() là trung điểm
là trung điểm ![]() nên
nên ![]() .
.
=> ![]() .
.
