Slide bài giảng Toán 12 cánh diều Bài 2: Công thức xác suất toàn phần. Công thức Bayes
Slide điện tử Bài 2: Công thức xác suất toàn phần. Công thức Bayes. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của môn Toán 12 Cánh diều sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
CÔNG THỨC XÁC SUẤT TOÀN PHẦN. CÔNG THỨC BAYES
I. CÔNG THỨC XÁC SUẤT TOÀN PHẦN
Hoạt động 1: Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, ..., 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét các biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
a) Viết các tập con của không gian mẫu tương ứng với các biến cố ![]()
b) So sánh:
![]()
Từ đó, hãy chứng tỏ rằng:
![]()
c) So sánh:
![]()
![]()
Từ đó, hãy chứng tỏ rằng:
![]()
Trả lời rút gọn:
a)
![]()
Biến cố A: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 3"
![]()
![]()
Biến cố B: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 4"
![]()
![]()
Biến cố A∩B: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 3 và 4" (chia hết cho 12)
![]()
![]()
Biến cố A∩B̅: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 3 nhưng không chia hết cho 4"
![]()
![]()
b) Ta có:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Vậy ![]()
c)
![]()
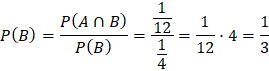
![]()
Vậy ![]()
- So sánh
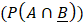 và
và 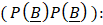
![]()
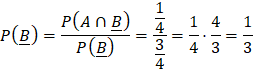
![]()
Vậy ![]()
![]()
Vậy:
![]()
Vận dụng 1: Hãy giải bài toán trong phần mở đầu bằng cách lập bảng thống kê như trong Ví dụ 2, biết rằng cả hai nhà máy sản xuất được 10 000 linh kiện.
Trả lời rút gọn:
Số linh kiện ở nhà máy 1:
![]()
Số linh kiện đạt tiêu chuẩn ở nhà máy 1:
![]()
Số linh kiện không đạt tiêu chuẩn ở nhà máy I:
![]()
Số link kiện ở nhà máy 2:
![]()
Số linh kiện đạt tiêu chuẩn ở nhà máy 2:
![]()
Số linh kiện không đạt tiêu chuẩn ở nhà máy 2:
![]()
| Linh kiện đạt tiêu chuẩn | Linh kiện không đạt tiêu chuẩn | |
| Nhà máy 1 | 4950 | 550 |
| Nhà máy 2 | 3985 | 585 |
A: biến cố linh kiện được lấy ra là sản phẩm của nhà máy I.
A’: biến cố linh kiện được lấy ra là sản phẩm của nhà máy II.
B: biến cố linh kiện được lấy ra đạt tiêu chuẩn.
P(A) = ![]()
P(B/A) = ![]()
P(B/A’) = ![]()
Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là:
![]()
Vậy, xác suất để linh kiện được lấy ra đạt tiêu chuẩn là 0,8925 hoặc 89,25%
Vận dụng 2: Hãy giải bài toán trong phần mở đầu bằng phương pháp sử dụng sơ đồ hình cây như trong ví dụ 3:
Trả lời rút gọn:
A: biến cố linh kiện được lấy ra là sản phẩm của nhà máy I.
B: biến cố linh kiện được lấy ra là sản phẩm của nhà máy II
C: biến cố linh kiện được lấy ra đạt tiêu chuẩn.
D: biến cố linh kiện được lấy ra không đạt tiêu chuẩn.
Sơ đồ hình cây biểu diễn bài toán:
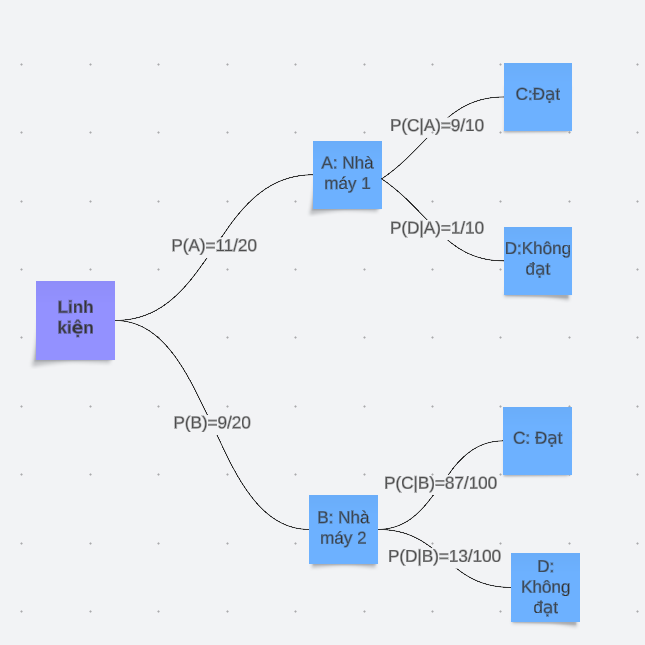
Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là:
![]()
II. CÔNG THỨC BAYES
Hoạt động 2: Xét hai biến cố A, B trong Hoạt động 1.
a) Tính: P(A), P(B), ![]() và P(B|A).
và P(B|A).
b) So sánh: P(B|A) và ![]()
Trả lời rút gọn:
![]()
Biến cố A: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 3"
![]()
![]()
Biến cố B: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 4"
![]()
![]()
a)
![]()
![]()
Biến cố A ∩ B: "Số xuất hiện trên thẻ được rút ra là số chia hết cho cả 3 và 4" (chia hết cho 12):
![]()
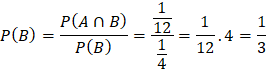
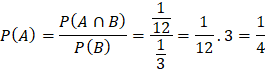
b)
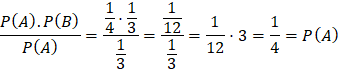
P(B|A) = ![]()
Vận dụng 3: Cho hai biến cố A, B sao cho P(A) = 0,4, P(B) = 0,8, P(B|A) = 0,3
Tính P(A|B).
Trả lời rút gọn:
![]()
Vận dụng 4: Được biết có 5% đàn ông bị mù màu, và 0,25% phụ nữ bị mù màu (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics - Understanding why and how, Springer, 2005). Giả sử số đàn ông bằng số phụ nữ. Chọn một người bị mù màu một cách ngẫu nhiên. Hỏi xác suất để người đó là đàn ông là bao nhiêu?
Trả lời rút gọn:
- D: Chọn ngẫu nhiên một người bị mù màu.
- M: Người đó là đàn ông.
- W: Người đó là phụ nữ.
- Xác suất để một người đàn ông bị mù màu: ![]()
- Xác suất để một người phụ nữ bị mù màu: ![]() .
.
- Giả sử số đàn ông bằng số phụ nữ: ![]() .
.
Tính xác suất để một người ngẫu nhiên bị mù màu ![]()
![]()
![]()
![]()
Xác suất để 1 người đàn ông bị mù màu:
![]()
![]()
![]()
Xác suất để một người ngẫu nhiên bị mù màu là đàn ông là khoảng ![]() 0.9524 hay 95,24%
0.9524 hay 95,24%
BÀI TẬP:
Bài tập 1: Cho hai biến cố A, B với P(B) = 0,6; P(A | B) = 0,7 và ![]() . Khi đó, P(A) bằng:
. Khi đó, P(A) bằng:
A. 0,7.
B. 0,4.
C. 0,58.
D. 0,52.
Trả lời rút gọn:
![]()
![]()
![]()
Vậy, P(A) bằng 0,58.
Đáp án đúng là:C. 0,58.
Bài tập 2: Có hai chiếc hộp, hộp I có 5 viên bi màu trắng và 5 viên bi màu đen, hộp II có 6 viên bi màu trắng và 4 viên bi màu đen, các viên bi có cùng kích thước và khối lượng.
a) Tính xác suất để viên bi được lấy ra là viên bi màu trắng.
b) Giả sử viên bi được lấy ra là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I.
Trả lời rút gọn:
- ![]() biến cố chọn hộp I.
biến cố chọn hộp I.
- ![]() : biến cố chọn hộp II.
: biến cố chọn hộp II.
- B :biến cố chọn được viên bi màu trắng.
- ![]()
- Xác suất lấy được viên bi màu trắng từ hộp I:
![]()
- Xác suất lấy được viên bi màu trắng từ hộp II:
![]()
![]()
![]()
![]()
![]()
Vậy, xác suất để viên bi được lấy ra là viên bi màu trắng là ![]() .
.
b)Giả sử viên bi được lấy ra là viên bi màu trắng, xác suất viên bi màu trắng đó thuộc hộp I là ![]()
![]()
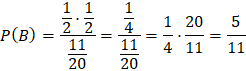
Vậy, xác suất để viên bi màu trắng đó thuộc hộp I là ![]() .
.
Bài tập 3: Một loại linh kiện do hai nhà máy số I, số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy I, II lần lượt là: 4%; 3%. Trong một lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số 1 và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó.
a) Tính xác suất để linh kiện được lấy ra là linh kiện tốt.
b) Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Xác suất linh kiện đó do nhà máy nào sản xuất là cao nhất?
Trả lời rút gọn:
- ![]() biến cố lấy sản phẩm từ nhà máy I
biến cố lấy sản phẩm từ nhà máy I
- ![]() biến cố lấy sản phẩm từ nhà máy II
biến cố lấy sản phẩm từ nhà máy II
- ![]() : biến cố sản phẩm lấy ra là sản phẩm tốt
: biến cố sản phẩm lấy ra là sản phẩm tốt
Xác suất chọn sản phẩm từ mỗi nhà máy:
![]()
![]()
- Nhà máy I: 4% tức ![]()
- Nhà máy II: 3% tức ![]()
![]()
![]()
![]()
![]()
![]()
Vậy, xác suất để linh kiện được lấy ra là linh kiện tốt là 0.966 hay 96.6%.
b)
- ![]() biến cố sản phẩm lấy ra là phế phẩm
biến cố sản phẩm lấy ra là phế phẩm
Xác suất lấy phế phẩm từ nhà máy 1:
![]()
Xác suất lấy phế phẩm từ nhà máy 2:
![]()
Mà
![]()
Vậy
![]()
![]()
![]()
Vậy, xác suất để linh kiện phế phẩm thuộc nhà máy II là cao nhất.
Bài tập 4: Một hộp có 20 chiếc thẻ cùng loại, trong đó có 2 chiếc thẻ màu xanh và 18 chiếc thẻ màu trắng. Bạn Châu rút thẻ hai lần một cách ngẫu nhiên, mỗi lần rút một thẻ và thẻ được rút ra không bỏ lại hộp. Tính xác suất để cả hai lần bạn Châu đều rút được thẻ màu xanh.
Trả lời rút gọn:
- ![]() Lần đầu rút được thẻ màu xanh.
Lần đầu rút được thẻ màu xanh.
-![]() Lần thứ hai rút được thẻ màu xanh.
Lần thứ hai rút được thẻ màu xanh.
Xác suất bạn Châu rút được 2 thẻ màu xanh: ![]()
Xác suất để lần đầu rút được thẻ màu xanh:
![]()
Xác suất để lần thứ hai rút được thẻ màu xanh, biết rằng lần đầu đã rút được thẻ màu xanh:
![]()
Xác suất để cả hai lần đều rút được thẻ màu xanh:
![]()
Vậy, xác suất để cả hai lần bạn Châu đều rút được thẻ màu xanh là ![]() .
.
Bài tập 4: Năm 2001, Cộng đồng châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Không có xét nghiệm nào cho kết quả chính xác 100%. Một loại xét nghiệm, mà ở đây ta gọi là xét nghiệm A, cho kết quả như sau: khi con bò bị bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm A là 70%, còn khi con bò không bị bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là 10%. Biết rằng tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1 000 000 con (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics-Understanding why and how, Springer, 2005). Hỏi khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là bao nhiêu?
Trả lời rút gọn:
-B: biến cố một con bò bị bệnh bò điên
-![]() : biến cố 1 con bò không bị bệnh bò điên
: biến cố 1 con bò không bị bệnh bò điên
- T: biến cố 1 con bò phản ứng dương tính.
- Xác suất một con bò bị bệnh bò điên: ![]()
- Xác suất một con bò không bị bệnh bò điên: ![]()
- Xác suất xét nghiệm cho kết quả dương tính nếu bò bị bệnh: ![]()
- Xác suất xét nghiệm cho kết quả dương tính nếu bò không bị bệnh:![]()
Xác suất để một con bò bị bệnh bò điên khi xét nghiệm cho kết quả dương tính, tức là ![]()
![]()
Trong đó:
![]()
![]()
Tính ![]()
![]()
Xác suất để một con bò ở Hà Lan bị mắc bệnh bò điên khi xét nghiệm A cho kết quả dương tính là khoảng 0.000091, hay 0.0091%.
