Slide bài giảng Toán 12 cánh diều Bài 2: Nguyên hàm của một số hàm số sơ cấp

Tóm lược nội dung

NGUYÊN HÀM CỦA MỘT SỐ HÀM SỐ SƠ CẤP

I. NGUYÊN HÀM CỦA HÀM SỐ LŨY THỪA

Hoạt động 1: Hàm số có là nguyên hàm của hàm số hay không?

Trả lời rút gọn:

là nguyên hàm của hàm số vì

Vận dụng 1: Tìm:

Trả lời rút gọn:

Vận dụng 2: Tìm:

a)  

b)

Trả lời rút gọn:

a)

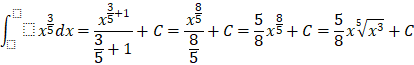
b)

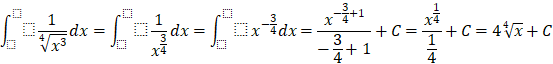
II. NGUYÊN HÀM CỦA HÀM SỐ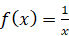

Hoạt động 2: a) Tính đạo hàm của hàm số trên khoảng (0;+∞)

b) Tính đạo hàm của hàm số trên khoảng (0;+∞)

Trả lời rút gọn:

a)  trên khoảng (0;+∞)

b) trên khoảng (-∞;0)

Vận dụng 3: Tìm

Trả lời rút gọn:

III. NGUYÊN HÀM CỦA HÀM SỐ LƯỢNG GIÁC 

Hoạt động 3: a) Hàm số có là nguyên hàm của hàm số hay không?

b) Hàm số có là nguyên hàm của hàm số hay không?

c) Với , , hàm số có là nguyên hàm của hàm số  hay không?

d) Với , , hàm số có là nguyên hàm của hàm số  hay không?

Trả lời rút gọn:

a) Hàm số là nguyên hàm của hàm số vì

b) Hàm số là nguyên hàm của hàm số vì

c)

Tính đạo hàm của :

Do đó hàm số là nguyên hàm của hàm số  với ,

d)

Tính đạo hàm của :

Với , , hàm số là nguyên hàm của hàm số  .

Vận dụng 4: Tìm:

a)

b)

Trả lời rút gọn:

a)

b)

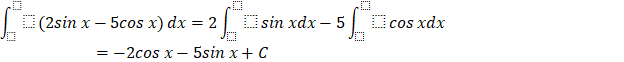
Vận dụng 5: Tìm:

a)

b)

Trả lời rút gọn:

a)

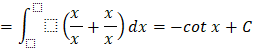
b)

IV. NGUYÊN HÀM CỦA HÀM SỐ MŨ 

Hoạt động 4: Tính đạo hàm của hàm số Từ đó nêu một nguyên hàm của hàm số

Trả lời rút gọn:

Đạo hàm của hàm số là . 

là một nguyên hàm của .

Vận dụng 6: Tìm: 

a)

b)

Trả lời rút gọn:

a)

b)

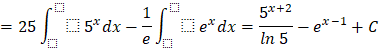
GIẢI BÀI TẬP CUỐI SÁCH GIÁO KHOA

Bài tập 1:  bằng:

A.

B.

C.

D.

Trả lời rút gọn:

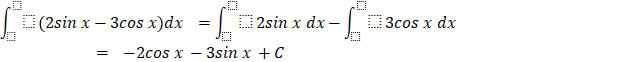
D

Bài tập 2:  bằng:

A.

B.

C.

D.

Trả lời rút gọn:

C.

Bài tập 3:  Nguyên hàm của hàm số bằng:

A.

B.

C.

D.

Trả lời rút gọn:

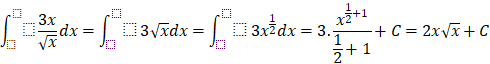
D.

Bài tập 4: Nguyên hàm của hàm số bằng:

A.

B.

C.

D.

Trả lời rút gọn:

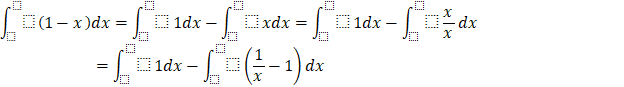
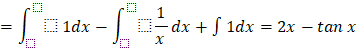
B. 

Bài tập 5: Tìm:

a)

b)

c)

d)

Trả lời rút gọn:

a)

b)

c)

d)

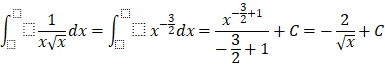
Bài tập 6: Tìm:

a.

b.

c.

d.

Trả lời rút gọn:

a)

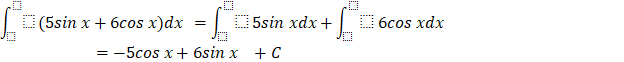
b)

c)

d)

Bài tập 7: Cây cà chua khi trồng có chiều cao 5 cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được cho bởi hàm số

Trong đó t tính theo tuần, v(t) tính theo centimet/tuần. Gọi h(t) (tính bằng centimet) là độ cao của cây cà chua ở tuần thứ t. (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-I, Cornelsen 2016).

a) Viết công thức xác định hàm số h(t) (t ≥ 0).

b) Giai đoạn tăng trưởng của cây cà chua đó kéo dài bao lâu?

c) Chiều cao tối đa của cây là bao nhiêu centimet?

d) Vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua đó cao bao nhiêu centimet?

Trả lời rút gọn:

a) Để xác định hàm số h(t), ta tính nguyên hàm của hàm v(t):

Thay t = 0 vào h(t):

=> C=5. Hàm số h(t) (t ≥ 0):

b) Giai đoạn tăng trưởng của cây cà chua kéo dài cho đến khi tốc độ tăng trưởng v(t) bằng 0. Ta có:

Phương trình có nghiệm t=0 và t=10. Vì vậy, giai đoạn tăng trưởng kéo dài từ tuần 1 đến tuần thứ 10. 

c) Chiều cao tối đa của cây cà chua có được khi nó ở tuần cuối của giai đoạn tăng trưởng. Vì giai đoạn tăng trưởng kéo dài đến tuần thứ 10, vì vậy chiều cao tối đa của cây sẽ đạt được khi t=10:

Vậy chiều cao tối đa của cây cà chua là 88,33cm.

d) Để tìm thời điểm cây cà chua phát triển nhanh nhất, ta cần tính giá trị của t mà tại t, v(t) đạt giá trị cực đại

khi . Thay giá trị t vào biểu thức

Vậy tại tuần thứ cây cà chua có tốc độ tăng trưởng lớn nhất.

Bài tập 8: Một quần thể vi khuẩn ban đầu gồm 500 vi khuẩn, sau đó bắt đầu tăng trưởng. Gọi P(t) là số lượng vi khuẩn của quần thể đó tại thời điểm t, trong đó t tính theo ngày (0 ≤ t ≤ 10). Tốc độ tăng trưởng của quần thể vi khuẩn đó được cho bởi hàm số trong đó k là hằng số. Sau 1 ngày, số lượng quần thể của vi khuẩn đó đã tăng lên thành 600 vi khuẩn. ( (Nguồn R.Larson and B. Edwards, Calculus 10e Cengage 2014). Tính số lượng vi khuẩn của quần thể đó sau 7 ngày (làm tròn kết quả đến hàng đơn vị).

Trả lời rút gọn:

Số lượng vi khuẩn tăng trưởng sẽ được tính bởi hàm P(t), với P(t) là nguyên hàm của hàm P’(t):

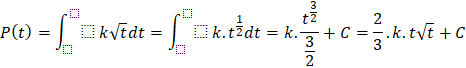
C=500

Sau 1 ngày, số lượng vi khuẩn tăng thành 600:

Sau 7 ngày, số lượng vi khuẩn là:

Vậy số lượng vi khuẩn sau 7 ngày là 2352 vi khuẩn.