Slide bài giảng Toán 12 cánh diều Bài 3: Biểu thức tọa độ của các phép toán vectơ
Slide điện tử Bài 3: Biểu thức tọa độ của các phép toán vectơ. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của môn Toán 12 Cánh diều sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 3: BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTO
I. BIỂU THỨC TỌA ĐỘ CỦA PHÉP CỘNG HAI VECTO, PHÉP TRỪ HAI VECTO, PHÉP NHÂN MỘT SỐ VỚI MỘT VECTO
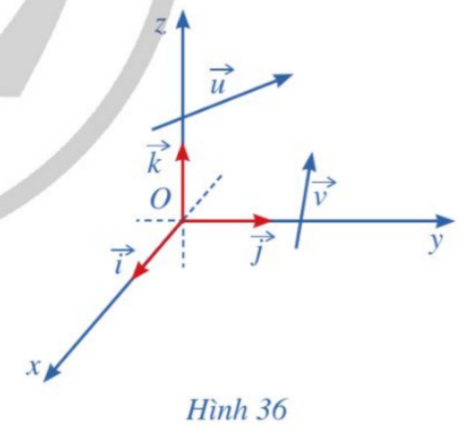
Hoạt động 1: Trong không gian với hệ tọa độ ![]() (Hình 36), cho hai vecto
(Hình 36), cho hai vecto ![]() và
và ![]() .
.
- Biểu diễn các vecto
 ,
, 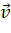 theo ba vecto
theo ba vecto 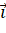 ,
, 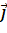 ,
,  .
. - Biểu diễn các vecto
 ,
, 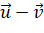 ,
,  theo ba vecto
theo ba vecto  ,
, 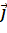 ,
, 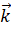 .
. - Tìm tọa độ các vecto
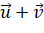 ,
,  ,
,  .
.
Trả lời rút gọn:
-
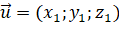 nên
nên 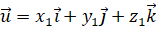 .
.
![]() nên
nên ![]() .
.
![]()
![]()
![]()
![]() (
(![]() ).
).
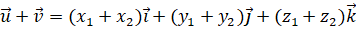 .
.
Do đó, tọa độ của vecto ![]() là
là ![]() .
.
![]()
Do đó, tọa độ của vecto ![]() là
là ![]() .
.
![]()
Do đó, tọa độ của vecto ![]() là
là ![]() .
.
Luyện tập 1: Cho ![]() ,
, ![]() ,
, ![]() . Tìm tọa độ của vecto
. Tìm tọa độ của vecto ![]() .
.
- Cho ba điểm
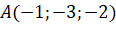 ,
, 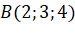 ,
,  . Chứng minh rằng ba điểm
. Chứng minh rằng ba điểm 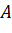 ,
,  ,
, 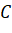 thẳng hàng.
thẳng hàng.
Trả lời rút gọn:
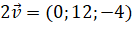 ,
, 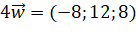 .
.
Do đó, ![]() .
.
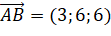 ,
,  .
.
![]()
=> ![]() .
.
Do đó, hai vecto ![]() và
và ![]() cùng phương.
cùng phương.
Suy ra hai đường thẳng ![]() và
và ![]() trùng nhau hay ba điểm
trùng nhau hay ba điểm ![]() ,
, ![]() ,
, ![]() thẳng hàng.
thẳng hàng.
II. TỌA ĐỘ TRUNG ĐIỂM ĐOẠN THẲNG. TỌA ĐỘ TRỌNG TÂM TAM GIÁC
Hoạt động 2: a,Trong không gian với hệ tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() và
và ![]() . Gọi
. Gọi ![]() là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng ![]() .
.
- Biểu diễn vecto
 theo hai vecto
theo hai vecto 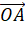 và
và 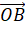 .
. - Tính tọa độ của điểm
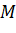 theo tọa độ của các điểm
theo tọa độ của các điểm  và
và 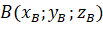 .
.
- Trong không gian với hệ tọa độ
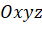 , cho tam giác
, cho tam giác 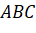 có trọng tâm
có trọng tâm  .
.
- Biểu diễn vecto
 theo ba vecto
theo ba vecto 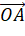 ,
,  ,
, 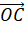 .
. - Tính tọa độ của điểm
 theo tọa độ của các điểm
theo tọa độ của các điểm 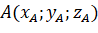 ,
,  ,
,  .
.
Trả lời rút gọn:
- Vì
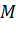 là trung điểm của
là trung điểm của 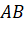 nên với điểm
nên với điểm 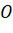 ta có:
ta có:  .
. - Ta có
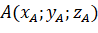 và
và 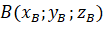 nên
nên  và
và 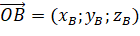 .
.
![]() .
.
=> 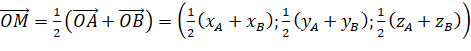 .
.
Do đó, 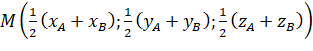 .
.
- Vì
 là trọng tâm của tam giác
là trọng tâm của tam giác  nên với điểm
nên với điểm 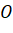 ta có:
ta có:

- Ta có:
 ,
, 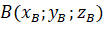 và
và 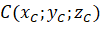 .
.
=> ![]() ,
, ![]() và
và ![]() .
.
Khi đó, ![]() .
.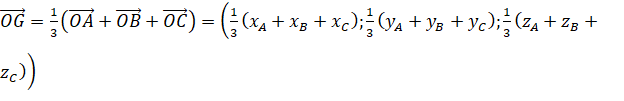
Do đó, 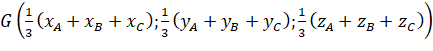 .
.
Luyện tập 2: Cho ba điểm ![]() ,
, ![]() ,
, ![]() .
.
- Chứng minh rằng ba điểm
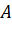 ,
, 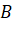 ,
, 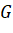 khổng thẳng hàng.
khổng thẳng hàng. - Tìm tọa độ điểm
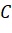 sao cho
sao cho 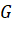 là trọng tâm của tam giác
là trọng tâm của tam giác 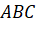 .
.
Trả lời rút gọn:
-
 ,
, 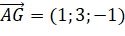 .
.
=> ![]() với
với ![]() nên hai vecto
nên hai vecto ![]() và
và ![]() không cùng phương.
không cùng phương.
Vậy ba điểm ![]() ,
, ![]() ,
, ![]() khổng thẳng hàng.
khổng thẳng hàng.
- Gọi tọa độ điểm
 là
là  . Vì
. Vì 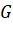 là trọng tâm của tam giác
là trọng tâm của tam giác 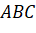 nên ta có:
nên ta có: 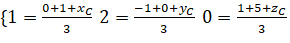
=> ![]() ,
, ![]() ,
, ![]() . Vậy
. Vậy ![]() .
.
III. BIỂU THỨC TỌA ĐỘ CỦA TÍCH VÔ HƯỚNG
Hoạt động 3: Trong không gian với hệ tọa độ ![]() , cho các vecto
, cho các vecto ![]() ,
, ![]() . Hãy biểu diễn các vecto
. Hãy biểu diễn các vecto ![]() ,
, ![]() theo ba vecto đơn vị
theo ba vecto đơn vị ![]() ,
, ![]() ,
, ![]() và tích vô hướng
và tích vô hướng ![]() .
.
Trả lời rút gọn:
![]() ,
, ![]() .
.
Do đó, ![]() ,
, ![]() .
.
![]()

Mà ![]() và
và ![]() (do là ba vecto đơn vị đôi một vuông góc với nhau).
(do là ba vecto đơn vị đôi một vuông góc với nhau).
Do đó, ![]() .
.
Luyện tập 3: Trong không gian với hệ tọa độ ![]() , cho tam giác
, cho tam giác ![]() có
có ![]() ,
, ![]() và
và ![]() . Chứng minh rằng tam giác
. Chứng minh rằng tam giác ![]() vuông tại
vuông tại ![]() .
.
Trả lời rút gọn:
![]() ,
, ![]()
Nhận thấy ![]() , do đó
, do đó ![]()
Suy ra hai vecto ![]() và
và ![]() vuông góc với nhau hay hai đường thẳng
vuông góc với nhau hay hai đường thẳng ![]() và
và ![]() vuông góc với nhau. Vậy tam giác
vuông góc với nhau. Vậy tam giác ![]() vuông tại
vuông tại ![]() .
.
IV. CÁCH TÌM TỌA ĐỘ CỦA MỘT VECTO VUÔNG GÓC VỚI HAI VECTO CHO TRƯỚC
Hoạt động 4: a,Cho hình lập phương ![]() có
có ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Hãy chỉ ra tọa độ của một vecto vuông góc với cả hai vecto
. Hãy chỉ ra tọa độ của một vecto vuông góc với cả hai vecto ![]() và
và ![]() .
.
b, Cho hai vecto ![]() và
và ![]() không cùng phương. Xét vecto
không cùng phương. Xét vecto ![]() .
.
- Tính
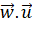 ,
, 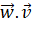 .
. - Vecto
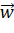 có vuông góc với cả hai vecto
có vuông góc với cả hai vecto  và
và 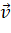 hay không?
hay không?
Giải chi tiết:
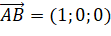 ,
,  .
.
Gọi tọa độ điểm ![]() là
là ![]() , ta có
, ta có ![]() .
.
Vì là ![]() hình lập phương nên
hình lập phương nên ![]() .
.
=>![]() ↔
↔ ![]() . Do đó,
. Do đó, ![]() .
.
![]() .
.
Ta thấy, ![]() ,
, ![]()
Vậy vecto ![]() vuông góc với cả hai vecto
vuông góc với cả hai vecto ![]() và
và ![]() .
.
![]()
![]() ;
;
![]()
![]() ;
;
- Vì
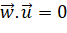 ,
, 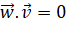 nên vecto
nên vecto 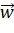 vuông góc với cả hai vecto
vuông góc với cả hai vecto 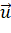 và
và 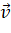 .
.
Luyện tập 4: Trong không gian với hệ tọa độ ![]() , cho hai vecto
, cho hai vecto ![]() và
và ![]() . Hãy chỉ ra tọa độ của một vecto
. Hãy chỉ ra tọa độ của một vecto ![]() khác
khác ![]() vuông góc với cả hai vecto
vuông góc với cả hai vecto ![]() và
và ![]() .
.
Trả lời rút gọn:
![]() .
.
Chọn ![]() .
.
Vậy vecto ![]() vuông góc với cả hai vecto
vuông góc với cả hai vecto ![]() và
và ![]() .
.
GIẢI BÀI TẬP
Bài 1: Trong không gian với hệ tọa độ ![]() , cho
, cho ![]() và
và ![]() . Tọa độ của vecto
. Tọa độ của vecto ![]() là:
là:
| A. | B. | C. | D. |
Trả lời rút gọn:
C.
![]() .
.
Bài 2: Trong không gian với hệ tọa độ ![]() , cho
, cho ![]() và
và ![]() . Góc giữa hai vecto
. Góc giữa hai vecto ![]() và
và ![]() bằng:
bằng:
| A. 60o | B. 120o | C. 150o | D. 30o |
Trả lời rút gọn:
A.
 .
.
=> ![]() .
.
Bài 3: Trong không gian với hệ tọa độ ![]() , cho
, cho ![]() ,
, ![]() ,
, ![]() .
.
- Tìm tọa độ của vecto
 .
. - Tìm tọa độ của vecto
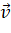 sao cho
sao cho 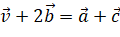 .
.
Trả lời rút gọn:

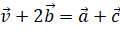 ↔
↔ 
![]() .
.
Bài 4: Trong không gian với hệ tọa độ ![]() , cho
, cho ![]() ,
, ![]() . Hãy chỉ ra tọa độ của một vecto
. Hãy chỉ ra tọa độ của một vecto ![]() khác
khác ![]() vuông góc với cả hai vecto
vuông góc với cả hai vecto ![]() và
và ![]() .
.
Trả lời rút gọn:
![]() .
.
Chọn ![]() , ta có vecto
, ta có vecto ![]() vuông góc với cả hai vecto
vuông góc với cả hai vecto ![]() và
và ![]() .
.
Bài 5: Trong không gian với hệ tọa độ![]() , cho
, cho ![]() ,
, ![]() . Tính cosin của góc
. Tính cosin của góc ![]() .
.
Trả lời rút gọn:
 .
.
Bài 6: Trong không gian với hệ tọa độ ![]() , cho
, cho ![]() ,
, ![]() ,
, ![]() .
.
- Chứng minh rằng ba điểm
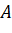 ,
,  ,
,  không thẳng hàng.
không thẳng hàng. - Tính chu vi tam giác
 .
. - Tìm tọa độ trọng tâm
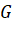 của tam giác
của tam giác  .
. - Tính
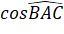 .
.
Trả lời rút gọn:
-
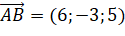 ,
, 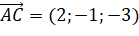 .
.
=> ![]() với
với ![]() , do đó hai vecto
, do đó hai vecto ![]() và
và ![]() không cùng phương.
không cùng phương.
Vậy ba điểm ![]() ,
, ![]() ,
, ![]() không thẳng hàng.
không thẳng hàng.
-
 ;
;
![]() .
.
![]() .
.
=> ![]() .
.
Chu vi tam giác ![]() là:
là: ![]() .
.
- Gọi tọa độ trọng tâm
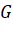 của tam giác
của tam giác  là
là  .
.
![]() ;
; ![]() ;
; ![]() .
.
Vậy ![]() .
.
-
 .
.
Do đó hai vecto ![]() và
và ![]() vuông góc với nhau hay hai đường thẳng
vuông góc với nhau hay hai đường thẳng ![]() và
và ![]() vuông góc với nhau nên
vuông góc với nhau nên ![]() . Vậy
. Vậy ![]() .
.
Bài 7: Cho hình hộp ![]() , biết
, biết ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Hãy chỉ ra tọa độ của một vecto khác
. Hãy chỉ ra tọa độ của một vecto khác ![]() vuông góc với cả hai vecto trong mỗi trường hợp sau:
vuông góc với cả hai vecto trong mỗi trường hợp sau:
|
|
Trả lời rút gọn:
-
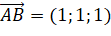 ,
, 
Vì ![]() là hình hộp nên
là hình hộp nên ![]() là hình bình hành, do đó:
là hình bình hành, do đó:
![]()
![]()
Vì ![]() là hình hộp nên
là hình hộp nên ![]() .
.
![]()
Chọn ![]() , vecto
, vecto ![]() vuông góc với cả hai vecto
vuông góc với cả hai vecto ![]() và
và ![]() .
.
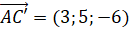 ,
, 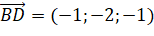 .
.
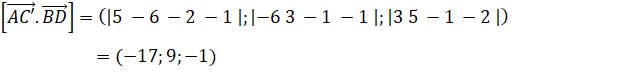
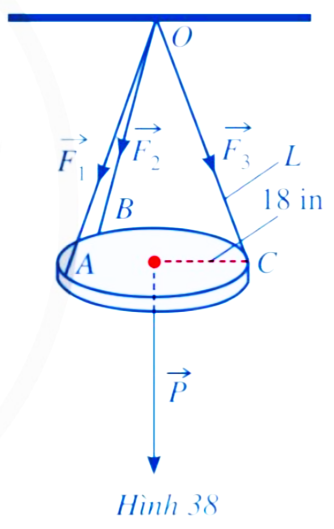
Chọn ![]() , vecto
, vecto ![]() vuông góc với cả hai
vuông góc với cả hai ![]() và
và ![]() .
.
Bài 8:
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm ![]() trên trần nhà lần lượt buộc vào ba điểm
trên trần nhà lần lượt buộc vào ba điểm ![]() ,
, ![]() ,
, ![]() trên đèn tròn sao cho tam giác
trên đèn tròn sao cho tam giác ![]() đều (Hình 38). Độ dài của ba đoạn dây
đều (Hình 38). Độ dài của ba đoạn dây ![]() ,
, ![]() ,
, ![]() đều bằng
đều bằng ![]() . Trọng lượng của chiếc đèn là 24 N và bán kính của chiếc đèn là 18 in (1 inch = 2,54 cm). Gọi
. Trọng lượng của chiếc đèn là 24 N và bán kính của chiếc đèn là 18 in (1 inch = 2,54 cm). Gọi ![]() là độ lớn của các lực căng
là độ lớn của các lực căng ![]() ,
, ![]() ,
, ![]() trên mỗi sợi dây. Khi đó,
trên mỗi sợi dây. Khi đó, ![]() là một hàm số với biến số là
là một hàm số với biến số là ![]() .
.
- Xác định công thức tính hàm số
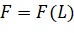 .
. - Khảo sát và vẽ đồ thị hàm số
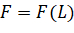 .
. - Tìm chiều dài tối thiểu của mỗi sợi dây, biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là 10 N.
Trả lời rút gọn:
- 18 in
 45,72 cm
45,72 cm  0,4572 m.
0,4572 m.
Gọi ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() . Vì tam giác
. Vì tam giác ![]() đều nên
đều nên ![]() là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác ![]() .
.
Do đó, ![]() m.
m.
Theo bài ra ta có ![]() nên
nên ![]() và
và ![]() .
.
=> ![]() .
.
Vì vậy, tồn tại hằng số ![]() sao cho:
sao cho: ![]() ;
; ![]() ;
; ![]() .
.
=> ![]() .
.
![]()
![]() (do
(do ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() nên
nên ![]() ).
).
=> ![]() .
.
Mặt khác ta lại có ![]() , với
, với ![]() là trọng lực tác dụng lên chiếc đèn. Mà trọng lượng tác dụng lên chiếc đèn là 24 N nên
là trọng lực tác dụng lên chiếc đèn. Mà trọng lượng tác dụng lên chiếc đèn là 24 N nên ![]() N.
N.
=> ![]() , tức là
, tức là ![]() .
.
Tam giác ![]() vuông tại
vuông tại ![]() (do
(do ![]() ) nên ta suy ra
) nên ta suy ra
![]() (m) với
(m) với ![]() .
.
Do đó, ![]() , suy ra
, suy ra ![]() .
.
![]() .
.
Vậy ![]() với
với ![]() .
.
- Xét hàm số
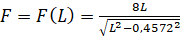 với
với 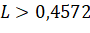 .
. 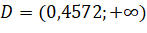 .
.
