Slide bài giảng Toán 12 cánh diều Bài 2: Tọa độ của vectơ
Slide điện tử Bài 2: Tọa độ của vectơ . Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của môn Toán 12 Cánh diều sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 2: TỌA ĐỘ CỦA VECTO
I. TỌA ĐỘ CỦA MỘT ĐIỂM
Hoạt động 1: Trong không gian, hãy vẽ:
- Ba trục số
 ,
, 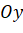 ,
, 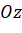 vuông góc với nhau từng đôi một và cắt nhau tại gốc
vuông góc với nhau từng đôi một và cắt nhau tại gốc 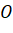 của mỗi trục.
của mỗi trục. - – Vecto
 xuất phát từ điểm gốc
xuất phát từ điểm gốc  , theo chiều dương của trục
, theo chiều dương của trục  và có độ dài bằng 1.
và có độ dài bằng 1.
– Vecto ![]() xuất phát từ điểm gốc
xuất phát từ điểm gốc ![]() , theo chiều dương của trục
, theo chiều dương của trục ![]() và có độ dài bằng 1.
và có độ dài bằng 1.
– Vecto ![]() xuất phát từ điểm gốc
xuất phát từ điểm gốc ![]() , theo chiều dương của trục
, theo chiều dương của trục ![]() và có độ dài bằng 1.
và có độ dài bằng 1.
Trả lời rút gọn:
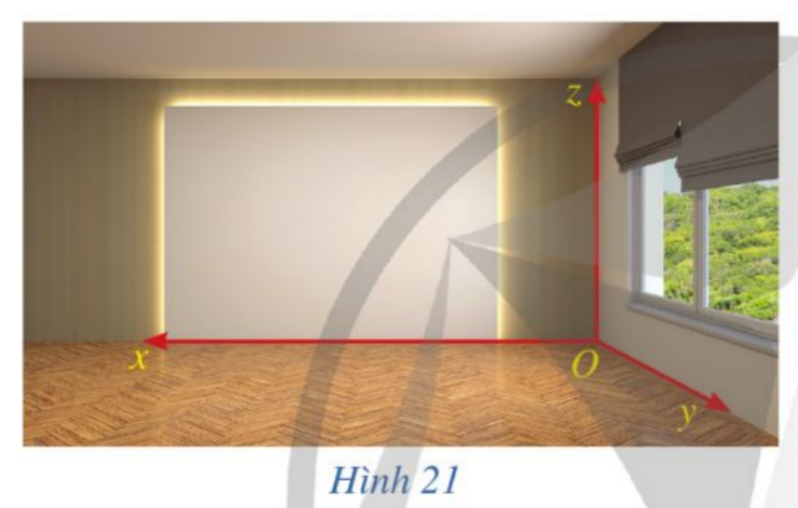
Luyện tập 1: Một căn phòng với hệ tọa độ ![]() được chọn như ở Hình 21. Cho biết bức tường phía sau của căn phòng nằm trong mặt phẳng tọa độ nào.
được chọn như ở Hình 21. Cho biết bức tường phía sau của căn phòng nằm trong mặt phẳng tọa độ nào.
Trả lời rút gọn:
Bức tường phía sau của căn phòng nằm trong mặt phẳng tọa độ ![]() .
.
Hoạt động 2: Cho điểm ![]() trong không gian với hệ tọa độ
trong không gian với hệ tọa độ ![]() . Gọi
. Gọi ![]() là hình chiếu của điểm
là hình chiếu của điểm ![]() trên mặt phẳng
trên mặt phẳng ![]() (Hình 22).
(Hình 22).
- Trong mặt phẳng
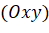 hãy cho biết:
hãy cho biết:
- Hình chiếu
 của điểm
của điểm  trên trục hoành
trên trục hoành  ứng với số nào trên trục
ứng với số nào trên trục  ?
? - Hình chiếu
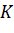 của điểm
của điểm 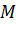 trên trục tung
trên trục tung 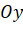 ứng với số nào trên trục
ứng với số nào trên trục 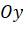 ?
?
- Hình chiếu
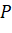 của điểm
của điểm  trên trục cao
trên trục cao 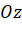 ứng với số nào trên trục
ứng với số nào trên trục 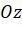 ?
?

Trả lời rút gọn:
- Hình chiếu
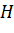 của điểm
của điểm 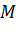 trên trục hoành
trên trục hoành  ứng với số 4 trên trục
ứng với số 4 trên trục  .
. - Hình chiếu
 của điểm
của điểm 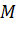 trên trục tung
trên trục tung  ứng với số 5 trên trục
ứng với số 5 trên trục  .
.
- Hình chiếu
 của điểm
của điểm  trên trục cao
trên trục cao 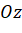 ứng với số 3 trên trục
ứng với số 3 trên trục 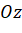 .
.
Luyện tập 2: Trong không gian với hệ tọa độ ![]() , cho điểm
, cho điểm ![]() . Gọi
. Gọi ![]() ,
, ![]() ,
, ![]() lần lượt là hình chiếu của điểm
lần lượt là hình chiếu của điểm ![]() trên các trục
trên các trục ![]() ,
, ![]() ,
, ![]() . Tìm tọa độ của các điểm
. Tìm tọa độ của các điểm ![]() ,
, ![]() ,
, ![]() .
.
Trả lời rút gọn:
Gọi ![]() ,
, ![]() ,
, ![]() .
.
Với ![]() , đặt
, đặt ![]() ,
, ![]() ,
, ![]()
 ;
; 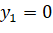 ;
;  (vì
(vì 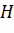 nằm trên trục
nằm trên trục  ). Do đó
). Do đó 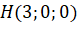 .
.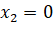 ;
; 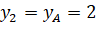 ;
;  (vì
(vì  nằm trên trục
nằm trên trục 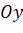 ). Do đó
). Do đó  .
. ;
; 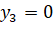 ;
; 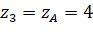 (vì
(vì 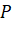 nằm trên trục
nằm trên trục 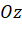 ). Do đó
). Do đó 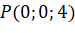 .
.
II. TỌA ĐỘ CỦA MỘT VECTO
Hoạt động 3: Cho điểm ![]() trong không gian với hệ tọa độ
trong không gian với hệ tọa độ ![]() .
.
- Vẽ vecto
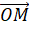 .
. - Nêu cách xác định tọa độ của điểm
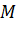 .
.
Trả lời rút gọn:
- Các bước vẽ vecto
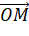 như sau:
như sau:
- Vẽ hệ trục tọa độ
 .
. - Lấy điểm
 bất kỳ trong hệ tọa độ
bất kỳ trong hệ tọa độ  .
. - Nối
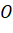 với
với 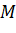 tạo thành vecto
tạo thành vecto 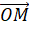 .
.
- Cách xác định tọa độ của điểm
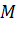 :
:
- Xác định hình chiếu
 của điểm
của điểm 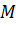 trên mặt phẳng
trên mặt phẳng 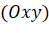 . Trong mặt phẳng tọa độ
. Trong mặt phẳng tọa độ 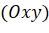 , tìm hoành độ
, tìm hoành độ  , tung độ
, tung độ  của điểm
của điểm 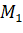 .
. - Xác định hình chiếu
 của điểm
của điểm 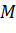 trên trục
trên trục 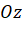 , điểm
, điểm  ứng với số
ứng với số 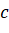 trên trục
trên trục  . Số
. Số 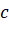 là cao độ của điểm
là cao độ của điểm 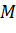 .
.
Vậy ![]() .
.
Luyện tập 3: Trong không gian với hệ tọa độ ![]() , cho
, cho ![]() . Tìm tọa độ điểm
. Tìm tọa độ điểm ![]() .
.
Trả lời rút gọn:
![]() . Do đó
. Do đó ![]() .
.
Hoạt động 4: Trong không gian với hệ tọa độ ![]() , cho vecto
, cho vecto ![]() (Hình 28). Hãy xác định điểm
(Hình 28). Hãy xác định điểm ![]() sao cho
sao cho ![]() (Hình 29).
(Hình 29).
Trả lời rút gọn:
Cách xác định điểm ![]() :
:
- Từ gốc tọa độ
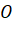 , dựng đường thẳng
, dựng đường thẳng 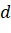 song song với giá của vecto
song song với giá của vecto 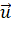 .
. - Trên
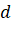 , lấy điểm
, lấy điểm 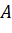 sao cho vecto
sao cho vecto 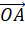 cùng hướng với vecto
cùng hướng với vecto  và
và 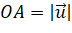 .
.
Vậy ta được điểm ![]() thỏa mãn
thỏa mãn ![]() .
.
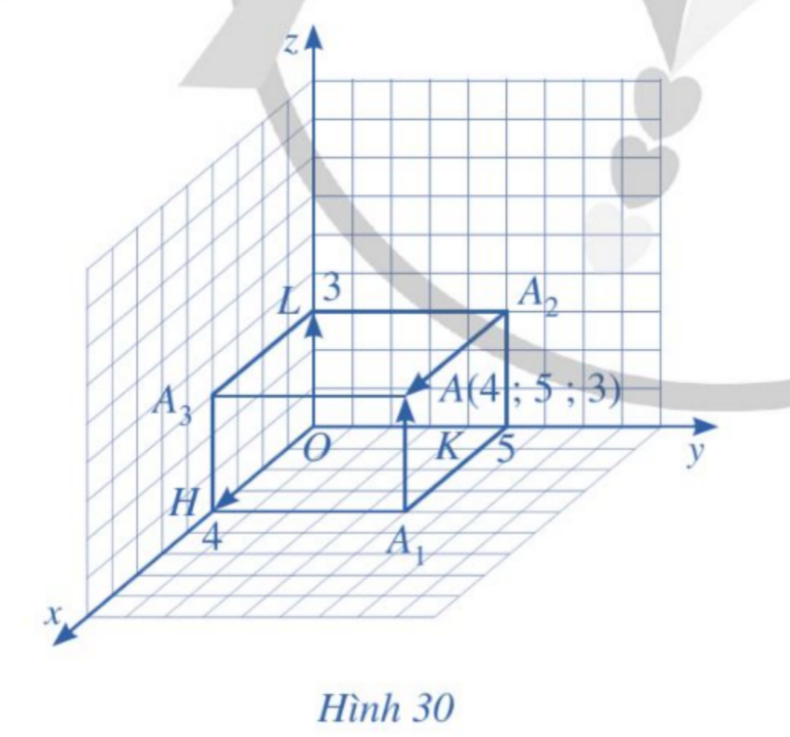
Luyện tập 4: Tìm tọa độ của các vecto ![]() ,
, ![]() ở Hình 30.
ở Hình 30.
Trả lời rút gọn:
![]() ,
, ![]() , mà
, mà ![]() và
và ![]() .
.
Do đó, ![]() và
và ![]() .
.
Hoạt động 5: Trong không gian với hệ tọa độ ![]() , cho vecto
, cho vecto ![]() (Hình 31). Lấy điểm
(Hình 31). Lấy điểm ![]() sao cho
sao cho ![]() .
.
- Tìm hoành độ, tung độ và cao độ của điểm
 .
. - Biểu diễn vecto
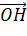 qua vecto
qua vecto 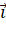 ; vecto
; vecto  qua vecto
qua vecto  ; vecto
; vecto 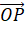 qua vecto
qua vecto 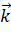 .
. - Biểu diễn vecto
 theo các vecto
theo các vecto 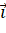 ,
, 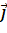 ,
, 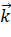 .
.

Trả lời rút gọn:
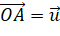 , mà
, mà 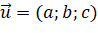 nên
nên 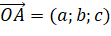 .
.
Do đó, ![]() . Vậy điểm
. Vậy điểm ![]() có hoành độ
có hoành độ ![]() , tung độ
, tung độ ![]() và cao độ
và cao độ ![]() .
.
 ;
;  ;
; 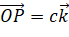 .
.- Theo quy tắc hình bình hành, ta có
 và
và  .
.
=> ![]() .
.
Mà ![]() . Do đó,
. Do đó, ![]() .
.
Luyện tập 5: Trong không gian với hệ tọa độ ![]() , cho vecto
, cho vecto ![]() và vecto
và vecto ![]() . Hãy tìm tọa độ của:
. Hãy tìm tọa độ của:
|
|
Trả lời rút gọn:
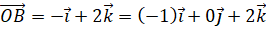 .
.
Do đó, ![]() . Vậy
. Vậy ![]() .
.
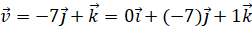 .
.
Do đó, ![]() .
.
Hoạt động 6: Trong không gian với hệ tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() ,
, ![]() (Hình 32).
(Hình 32).
- Biểu diễn mỗi vecto
 ,
, 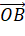 theo các vecto
theo các vecto 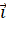 ,
,  và
và 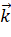 .
. - Tìm liên hệ giữa
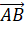 và
và  .
. - Từ đó, tìm tọa độ của vecto
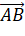 .
.

Trả lời rút gọn:
- Vì điểm
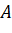 có tọa độ là
có tọa độ là 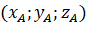 nên
nên 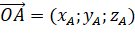 .
.
![]() .
.
Vì điểm ![]() có tọa độ là
có tọa độ là ![]() nên
nên ![]() .
.
![]() .
.
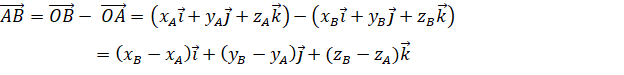
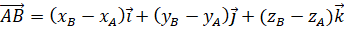 .
.
![]() .
.
Luyện tập 6: Trong không gian với hệ tọa độ ![]() , cho hình hộp
, cho hình hộp ![]() có
có ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Tìm tọa độ đỉnh ![]() của hình hộp
của hình hộp ![]() .
.
Trả lời rút gọn:
![]() .
.
Gọi tọa độ của điểm ![]() là
là ![]()
![]() .
.
Vì ![]() là hình hộp nên
là hình hộp nên ![]() là hình bình hành.
là hình bình hành.
Do đó, ![]()
![]() ↔
↔ ![]()
Khi đó, ![]() .
.
![]() .
.
Gọi tọa độ của điểm ![]() là
là ![]() , ta có
, ta có ![]() .
.
Vì ![]() là hình hộp nên
là hình hộp nên ![]() .
.
Do đó, ![]() ↔
↔ ![]() .
.
Vậy ![]() .
.
GIẢI CHI TIẾT
Bài 1: Trong không gian với hệ tọa độ ![]() , cho điểm
, cho điểm ![]() . Tọa độ của vecto
. Tọa độ của vecto ![]() là:
là:
Trả lời rút gọn:
A.
Bài 2: Trong không gian với hệ tọa độ ![]() , cho vecto
, cho vecto ![]() và điểm
và điểm ![]() . Biết
. Biết ![]() . Tọa độ của điểm
. Tọa độ của điểm ![]() là:
là:
| A. | B. | C. | D. |
Trả lời rút gọn:
B.
Bài 3: Trong không gian với hệ tọa độ ![]() , cho vecto
, cho vecto ![]() . Tọa độ của vecto
. Tọa độ của vecto ![]() là:
là:
| A. | B. | C. | D. |
Trả lời rút gọn:
A.
Bài 4: Trong không gian với hệ tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() và
và ![]() . Tọa độ của vecto
. Tọa độ của vecto ![]() là:
là:
| A. | B. | C. | D. |
Trả lời rút gọn:
B.
![]() .
.
Bài 5: Trong không gian với hệ tọa độ ![]() , cho vecto
, cho vecto ![]() và điểm
và điểm ![]() . Tọa độ điểm
. Tọa độ điểm ![]() thỏa mãn
thỏa mãn ![]() là:
là:
| A. | B. | C. | D. |
Trả lời rút gọn:
C.
Gọi tọa độ điểm ![]() là
là ![]() , ta có:
, ta có: ![]() .
.
Với ![]() thì
thì ![]() .
.
Vậy ![]() .
.
Bài 6: Trong không gian với hệ tọa độ ![]() , cho
, cho ![]() . Gọi
. Gọi ![]() ,
, ![]() ,
, ![]() lần lượt là hình chiếu của điểm
lần lượt là hình chiếu của điểm ![]() trên các mặt phẳng tọa độ
trên các mặt phẳng tọa độ ![]() ,
, ![]() ,
, ![]() . Tìm tọa độ của các điểm
. Tìm tọa độ của các điểm ![]() ,
, ![]() ,
, ![]() .
.
Trả lời rút gọn:
Gọi ![]() ,
, ![]() và
và ![]() .
.
Với ![]() , đặt
, đặt ![]() ,
, ![]() ,
, ![]() .
.
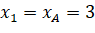 ;
; 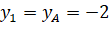 ;
; 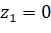 (vì
(vì  nằm trên mặt phẳng
nằm trên mặt phẳng  ).
).
![]() .
.
 ;
; 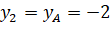 ;
; 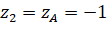 (vì
(vì 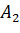 nằm trên mặt phẳng
nằm trên mặt phẳng 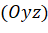 ).
).
![]() .
.
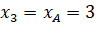 ;
;  ;
; 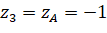 (vì
(vì 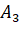 nằm trên mặt phẳng
nằm trên mặt phẳng  ).
).
![]() .
.
Bài 7: Trong không gian với hệ tọa độ ![]() , cho
, cho ![]() . Gọi
. Gọi ![]() ,
, ![]() ,
, ![]() lần lượt là hình chiếu của điểm
lần lượt là hình chiếu của điểm ![]() trên các trục
trên các trục ![]() ,
, ![]() ,
, ![]() . Tìm tọa độ của các điểm
. Tìm tọa độ của các điểm ![]() ,
, ![]() ,
, ![]() .
.
Trả lời rút gọn:
Gọi ![]() ,
, ![]() và
và ![]() .
.
Với ![]() , đặt
, đặt ![]() ,
, ![]() ,
, ![]() .
.
 ;
; 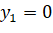 ;
; 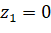 (vì
(vì  nằm trên trục
nằm trên trục 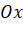 ).
).
![]() .
.
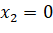 ;
;  ;
;  (vì
(vì 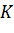 nằm trên trục
nằm trên trục 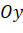 ).
).
![]() .
.
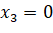 ;
; 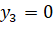 ;
; 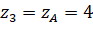 (vì
(vì 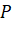 nằm trên trục
nằm trên trục  ).
).
![]() .
.
Bài 8: Trong không gian với hệ tọa độ ![]() , cho hình hộp
, cho hình hộp ![]() có
có ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Tìm tọa độ các đỉnh còn lại của hình hộp
. Tìm tọa độ các đỉnh còn lại của hình hộp ![]() .
.
Trả lời rút gọn:
![]() .
.
Gọi tọa độ của điểm ![]() là
là ![]() , ta có:
, ta có: ![]() .
.
Vì ![]() là hình hộp nên
là hình hộp nên ![]() là hình bình hành.
là hình bình hành.
Do đó, ![]() . Suy ra,
. Suy ra, ![]() ↔
↔ ![]()
Khi đó, ![]() .
.
![]() .
.
Gọi tọa độ của điểm ![]() là
là ![]() , ta có
, ta có ![]() .
.
![]() ↔
↔ ![]() ↔
↔ ![]()
![]() .
.
Gọi tọa độ của điểm ![]() là
là ![]() , ta có
, ta có ![]()
![]() ↔
↔ ![]() ↔
↔ ![]()
![]() .
.
Gọi tọa độ của điểm ![]() là
là ![]() , ta có
, ta có ![]()
![]() ↔
↔ ![]() ↔
↔ ![]()
![]() .
.
Bài 9: Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao 30 m và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn.
Mô hình thiết kế được xây dựng như sau: Trong hệ trục tọa độ ![]() (đơn vị độ dài trên mỗi trục là 1 m), các đỉnh của bốn chiếc cột lần lượt là các điểm
(đơn vị độ dài trên mỗi trục là 1 m), các đỉnh của bốn chiếc cột lần lượt là các điểm ![]() ,
, ![]() ,
, ![]() ,
, ![]() (Hình 34).
(Hình 34).
Giả sử ![]() là vị trí ban đầu của camera có cao độ bằng 25 và
là vị trí ban đầu của camera có cao độ bằng 25 và ![]() . Để theo dõi quả bóng đến vị trí
. Để theo dõi quả bóng đến vị trí ![]() , camera được hạ thấp theo phương thẳng đứng xuống điểm
, camera được hạ thấp theo phương thẳng đứng xuống điểm ![]() có cao độ bằng 19 (Nguồn: http://www.abiturloesung.de; Abitur Bayern 2016 Geometrie VI).
có cao độ bằng 19 (Nguồn: http://www.abiturloesung.de; Abitur Bayern 2016 Geometrie VI).
Tìm tọa độ của các điểm ![]() ,
, ![]() và của vecto
và của vecto ![]()
Trả lời rút gọn: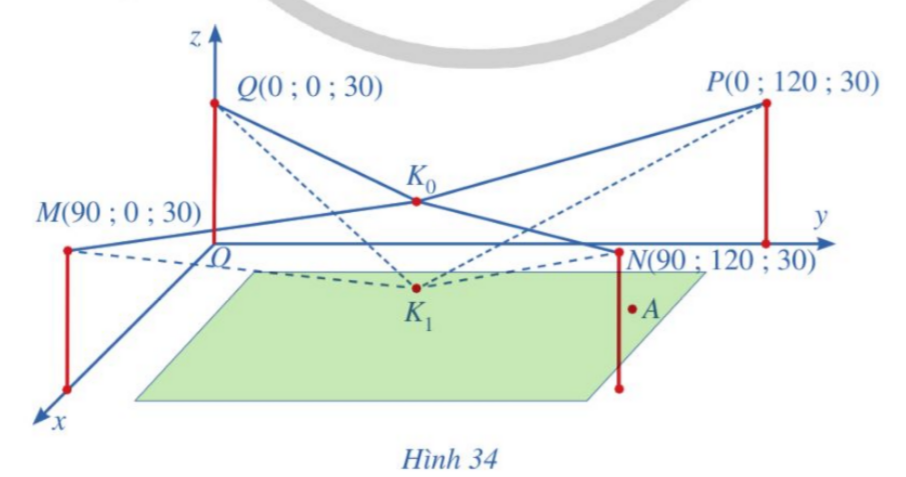
Gọi ![]() ,
, ![]() ,
, ![]() ,
, ![]() lần lượt là hình chiếu của
lần lượt là hình chiếu của ![]() ,
, ![]() ,
, ![]() ,
, ![]() lên mặt phẳng
lên mặt phẳng ![]() .
.
Ta thấy ![]() là hình hộp chữ nhật.
là hình hộp chữ nhật.
Gọi ![]() là giao hai đường chéo
là giao hai đường chéo ![]() và
và ![]() . Khi đó
. Khi đó ![]() .
.
Vì ![]() và camera được hạ thấp theo phương thẳng đứng từ điểm
và camera được hạ thấp theo phương thẳng đứng từ điểm ![]() xuống điểm
xuống điểm ![]() nên các điểm
nên các điểm ![]() ,
, ![]() ,
, ![]() ,
, ![]() thẳng hàng.
thẳng hàng.
Khi đó, các điểm ![]() ,
, ![]() ,
, ![]() ,
, ![]() có hoành độ và tung độ bằng nhau.
có hoành độ và tung độ bằng nhau.
Theo bài ra, cao độ của ![]() và
và ![]() lần lượt là 25 và 19.
lần lượt là 25 và 19.
Giả sử ![]() và
và ![]() . Ta có
. Ta có ![]() là hình hộp chữ nhật nên
là hình hộp chữ nhật nên ![]() , suy ra cao của
, suy ra cao của ![]() bằng 30. Do đó,
bằng 30. Do đó, ![]() .
.
![]() ,
, ![]()
Vì ![]() là giao hai đường chéo của hình chữ nhật
là giao hai đường chéo của hình chữ nhật ![]() nên
nên ![]() là trung điểm của
là trung điểm của ![]() .
.
=> ![]() ↔
↔ ![]() ↔
↔ ![]() .
.
Do vậy, ![]() ,
, ![]() và
và ![]() .
.


