Slide bài giảng Toán 12 cánh diều Bài 1: Phương trình mặt phẳng

Tóm lược nội dung

PHƯƠNG TRÌNH MẶT PHẲNG

I. VECTOR PHÁP TUYẾN. CẶP VECTOR CHỈ PHƯƠNG CỦA MẶT PHẲNG

1. Vector pháp tuyến

Hoạt động 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’ (Hình 2). Giá của vector có vuông góc với mặt phẳng ABCD hay không?

Trả lời rút gọn:

vuông góc với

vuông góc với

Vector vuông góc với mặt phẳng ABCD

Vận dụng 1: Trong không gian với hệ tọa độ Oxyz, hãy chỉ ra một vectơ pháp tuyến của:

a) Mặt phẳng (Oyz);

b) Mặt phẳng (Ozx).

Trả lời rút gọn:

a) Vector có giá là trục Ox và Ox vuông góc với (Oyz) nên =(1;0;0) là một vector pháp tuyến của mặt phẳng (Oyz)

b) Vector =(0,1;0) có giá là trục Oy và Oy vuông góc với (Ozx) nên =(0;1;0) là một vector pháp tuyến của mặt phẳng (Ozx)

2. Cặp vector chỉ phương

Hoạt động 2: Cho hình hộp ABCD.A'B'C'D'. Cho biết hai vectơ có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vectơ  và mặt phẳng (ABCD) (Hình 5).

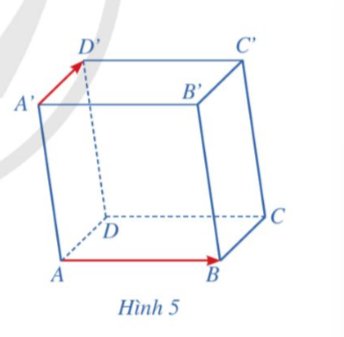
Trả lời rút gọn:

vuông góc với  . Mà  // . Vậy hai vector  không cùng phương.

Vector  nằm trong mặt phẳng ABCD

Vector  nằm ngoài mặt phẳng ABCD và song song với mặt phẳng.

Vận dụng 2: Trong không gian với hệ tọa độ Oxyz, hãy chỉ ra một cặp vectơ chỉ phương của mỗi mặt phẳng (Oxy), (Oyz), (Ozx).

Trả lời rút gọn:

Mặt phẳng (Oxy) đi qua trục Ox, Oy và vuông góc với trục Oz. Do đó, hai vectơ chỉ phương của mặt phẳng (Oxy) là:

- i = (1, 0, 0)

- j = (0, 1, 0)

Mặt phẳng (Oyz) đi qua trục Oy, Oz và vuông góc với trục Ox. Do đó, hai vectơ chỉ phương của mặt phẳng (Oyz) là:

- j = (0, 1, 0)

- k = (0, 0, 1)

Mặt phẳng (Ozx) đi qua trục Ox, Oz và vuông góc với trục Oy. Do đó, hai vectơ chỉ phương của mặt phẳng (Ozx) là:

- i = (1, 0, 0)

- k = (0, 0, 1)

3. Xác định vector pháp tuyến của mặt phẳng khi biết cặp vector chỉ phương 

Hoạt động 3: Cho cặp vectơ chỉ phương a=(1;0;1) và b=(2;1;0) của mặt phẳng (P).

a) Hãy chỉ ra tọa độ của một vectơ n(n khác 0) vuông góc với cả hai vectơ a và b (Hình 6)

b) Vectơ n có là vectơ pháp tuyến của mặt phẳng (P) hay không?

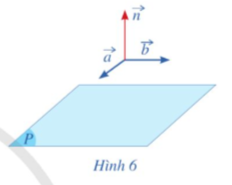
Trả lời rút gọn:

a)Tọa độ của một vectơ vuông góc với cả hai vectơ và

Thay tọa độ của các vectơ vào ta được:

Giải hệ phương trình này, ta được:

b) Vectơ pháp tuyến của mặt phẳng (P) là vectơ vuông góc với vectơ chỉ phương của mặt phẳng. Do đó, vectơ là vectơ pháp tuyến của mặt phẳng (P).

Vận dụng 3: Trong Ví dụ 3, vectơ   có là vectơ pháp tuyến của mặt phẳng (P) hay không? Vì sao?

Trả lời rút gọn:

Do đó, cũng là một vectơ pháp tuyến của mặt phẳng (P).

II. Phương trình tổng quát của mặt phẳng

Hoạt động 4: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm A(1;-1;2) và có vectơ pháp tuyến là Giả sử (M(x;y;z)) là một điểm tuỳ ý thuộc mặt phẳng (P) (Hình 7).

a) Tính tích vô hướng theo x, y, z.

b) Toạ độ (x; y, z) của điểm M có thoả mãn phương trình: hay không?

Trả lời rút gọn:

a)

là vectơ pháp tuyến của mặt phẳng (P).

A(1;-1;2) là một điểm thuộc mặt phẳng (P).

M(x;y;z) là một điểm tuỳ ý thuộc mặt phẳng (P).

Vậy, tích vô hướng theo x, y, z là x + 2y + 3z – 5.

b) Vì  ,là vector pháp tuyến của (P)

Vậy toạ độ (x; y, z) của điểm M có thoả mãn phương trình:

Vận dụng 4: Chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng sau:

a) (P): x-y=0;

b) (Q): z-2=0

Trả lời rút gọn:

a) Mặt phẳng (P):

Vậy mặt phẳng P nhận   làm vector pháp tuyến

b) Mặt phẳng (Q):

Vậy mặt phẳng P nhận   làm vector pháp tuyến

III. LẬP PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG BIẾT MỘT SỐ ĐIỀU KIỆN

1. Lập phương trình tổng quát của mặt phẳng đi qua 1 điểm và biết vector pháp tuyến 

Hoạt động 5: Cho mặt phẳng (P) đi qua điểm có   là vectơ pháp tuyến. Giả sử M(x;y;z) là một điểm bất kì thuộc mặt phẳng (P) (Hình 9).

a) Tính tích vô hướng  

b) Hãy biểu diễn theo và A,B,C

Trả lời rút gọn:

a) 

Vector là vectơ từ điểm đến điểm trên mặt phẳng (P). Vector này có phương trình:

b) Biểu diễn theo và

Vận dụng 5: Cho hai điểm M(2; 1; 0) và N(3; 0; 1). Lập phương trình mặt phẳng trung trực của đoạn thẳng MN.

Trả lời rút gọn:

Vectơ chỉ phương của đường thẳng MN là  

Mặt phẳng trung trực của đoạn thẳng MN là mặt phẳng vuông góc với vectơ và đi qua trung điểm P.

Phương trình tổng quát của một mặt phẳng là:

   Trong đó, là vectơ pháp tuyến của mặt phẳng. Ở đây, vectơ pháp tuyến chính là . Ta có phương trình mặt phẳng:

Phương trình đi qua trung điểm :

   Vậy phương trình mặt phẳng là:

2. Lập phương trình tổng quát của mặt phẳng đi qua 1 điểm và biết được cặp vector chỉ phương

Hoạt động 6: Cho mặt phẳng (P) đi qua điểm I(1:3:-2) có cặp vectơ chỉ phương là và

a) Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (P).

b) Lập phương trình mặt phẳng (P) đi qua điểm (1; 3;-2), biết vectơ pháp tuyến

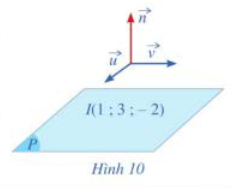
Trả lời rút gọn:

a) Vectơ pháp tuyến của mặt phẳng (P) là tích có hướng của hai vectơ chỉ phương và

Vậy một vectơ pháp tuyến của mặt phẳng (P) là

b)

Phương trình mặt phẳng (P) đi qua điểm và có là:

Vậy phương trình mặt phẳng (P) là

Vận dụng 6:  Cho mặt phẳng (P) đi qua điểm (). Lập phương trình mặt phẳng (P), biết mặt phẳng đó:

a) Vuông góc với trục Ox,

b) Vuông góc với trục Oy;

c) Vuông góc với trục Oz.

Trả lời rút gọn:

a) Nếu mặt phẳng vuông góc với trục (Ox), thì có là vector pháp tuyến. Do đó, phương trình có dạng:

b) Nếu mặt phẳng vuông góc với trục (Oy), thì có là vector pháp tuyến. Do đó, phương trình có dạng:

c) Nếu mặt phẳng vuông góc với trục (Oz), thì có là vector pháp tuyến. Do đó, phương trình có dạng:

Hoạt động 7: Cho ba điểm cùng thuộc mặt phẳng (P) (Hình 11).

a) Tìm toạ độ của các vectơ Từ đó hãy chứng tỏ rằng ba điểm H, I, K không thẳng hàng.

b) Lập phương trình mặt phẳng (P) đi qua điểm (H(-1;1;2) biết cặp vectơ chỉ phương là

Trả lời rút gọn:

a) 

Chúng ta kiểm tra xem có tồn tại số k nào sao cho:

Do các phương trình mâu thuẫn với nhau, không tồn tại số k nào thỏa mãn cả ba phương trình, do đó hai vectơ và không cùng phương. Vì vậy, ba điểm H, I, K không thẳng hàng.

b) Phương trình mặt phẳng (P) có dạng:

Trong đó, (a, b, c) là tọa độ của một vectơ pháp tuyến của mặt phẳng, được xác định bằng tích có hướng của hai vectơ chỉ phương và

Do đó, phương trình mặt phẳng có dạng:

Vậy phương trình mặt phẳng (P) là:

Vận dụng 7: Lập phương trình mặt phẳng đi qua ba điểm M(1; 2; 1), N(0; 3; 2) và P(-1; 0; 0)

Trả lời rút gọn:

Để lập phương trình mặt phẳng đi qua ba điểm và chúng ta sẽ thực hiện các bước sau:

 Tìm tọa độ của các vectơ và

Tìm tọa độ của vectơ pháp tuyến của mặt phẳng

Phương trình mặt phẳng có dạng:

Trong đó (a, b, c) là tọa độ của vectơ pháp tuyến và là tọa độ của một điểm nằm trên mặt phẳng, ví dụ như điểm

Vậy phương trình mặt phẳng đi qua ba điểm và là:

Phương trình mặt phẳng đi qua ba điểm A(2, 0, 0), B(0, 3, 0), và C(0, 0, 4) là:

IV. ĐIỀU KIỆN SONG SONG, VUÔNG GÓC CỦA 2 MẶT PHẲNG

1. Điều kiện song song của 2 mặt phẳng

Hoạt động 8: Cho mặt phẳng (P₁):

Và mặt phẳng (P₂):

a) Gọi lần lượt là vectơ pháp tuyến của hai mặt phẳng (Hình 14). Tìm liên hệ giữa và

b) Tìm hệ số tự do D₁, D₂ lần lượt của 2 phương trình (1), (2). So sánh D₁ và 2D₂

c) Nêu vị trí tương đối của 2 mặt phẳng (P₁), (P₂).

Trả lời rút gọn:

a) 

Vậy:

b) Phương trình mặt phẳng

Ở đây, hệ số tự do

Phương trình mặt phẳng

Ở đây, hệ số tự do

So sánh và

Như vậy,

c) 

Vì và tỉ lệ với nhau, hai mặt phẳng này song song hoặc trùng nhau.

Do hai mặt phẳng này song song và không trùng nhau.

Vận dụng 9: Chứng minh rằng các mặt phẳng

(P): (x-m=0)

(Q): (y-m=0)

(R): (z-m=0)

lần lượt song song với các mặt phẳng (Oyz), (Ozx), (Oxy).

Trả lời rút gọn:

Xét mặt phẳng (P) và (Oyz) có phương trình lần lượt là 

Ta thấy 2 mặt phẳng đều có vector chỉ phương . Tuy nhiên hệ số của 2 phương trình khác nhau . Vậy (P)//(Oyz)

Xét mặt phẳng (Q) và (Oxz) có phương trình lần lượt là 

Ta thấy 2 mặt phẳng đều có vector chỉ phương . Tuy nhiên hệ số của 2 phương trình khác nhau . Vậy (Q)//(Oxz)

Xét mặt phẳng (R) và (Oxy) có phương trình lần lượt là 

Ta thấy 2 mặt phẳng đều có vector chỉ phương . Tuy nhiên hệ số của 2 phương trình khác nhau . Vậy (R)//(Oxy)

2. Điều kiện vuông góc của 2 mặt phẳng

Hoạt động 9: Cho mặt phẳng có phương trình tổng quát là:

và mặt phẳng có phương trình tổng quát là:

Gọi lần lượt là vectơ pháp tuyến của hai mặt phẳng Hai vectơ có vuông góc với nhau hay không?

Trả lời rút gọn:

Vậy hai vectơ vuông góc với nhau.

Vận dụng 10: Chứng minh rằng hai mặt phẳng (Ozx) và (P): x + 2z - 3 = 0 vuông góc với nhau.

Trả lời rút gọn:

Ta có phương trình của Ozx:

=>

Vậy hai mặt phẳng (Ozx) và (P): x + 2z - 3 = 0 vuông góc với nhau.

V. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG

Hoạt động 10: Cho mặt phẳng (P) có phương trình tổng quát là với là vecto pháp tuyến. Cho điểm Gọi là hình chiếu vuông góc của điểm M trên mặt phẳng (P)

a) Tính toạ độ của theo

b) Nêu nhận xét về phương của hai vectơ           

Từ đó, hãy suy ra rằng

=

c) Tính các độ dài theo A, B, C, D. Từ đó, hãy nêu công thức tính khoảng cách từ điểm M₀(2;3;4) đến mặt phẳng (P).

Trả lời rút gọn:

 a)

Gọi là hình chiếu vuông góc của điểm trên mặt phẳng (P).

b)  Vì H là hình chiếu vuông góc của trên mặt phẳng (P), nên vectơ phải song song với vectơ pháp tuyến .

Vì 2 vector song song nên:

=>

Do H nằm trên mặt phẳng (P), ta có phương trình của mặt phẳng (P):

=>

Vậy:

c) 

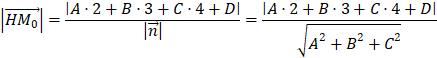
Do đó, khoảng cách từ là khoảng cách từ M₀ đến mặt phẳng (P) là:

Công thức tính khoảng từ điểm M₀(2;3;4) đến mặt phẳng (P):

Hoạt động 11: Chứng minh rằng khoảng cách từ điểm M(a, b, c) đến các mặt phẳng (Oyz), (Ozx), (Oxy) lần lượt bằng |a|,|b|,|c|

Trả lời rút gọn:

•  Khoảng cách từ điểm M đến mặt phẳng (Oyz):

phương trình mặt phẳng (Oyz): x=0 

Khoảng cách từ điểm M đến mặt phẳng (Oyz):

• Khoảng cách từ điểm M đến mặt phẳng (Ozx):

phương trình mặt phẳng (Ozx): y=0 

Khoảng cách từ điểm M đến mặt phẳng (Oyz):

• Khoảng cách từ điểm M đến mặt phẳng (Oxy):

phương trình mặt phẳng (Oxy): z=0 

Khoảng cách từ điểm M đến mặt phẳng (Oxy):

 Vận dụng 12: Cho mặt phẳng và mặt phẳng

a) Chứng minh rằng:

b) Tính khoảng cách giữa hai mặt phẳng song song,

Trả lời rút gọn:

a) Vecto pháp tuyến của mặt phẳng

Vecto pháp tuyến của mặt phẳng

Vậy, hai mặt phẳng song song với nhau.

b) Chọn điểm là 1 điểm thuộc P₁

Khoảng cách giữa M đến (P₂):

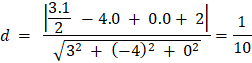
Do hai mặt phẳng là song song, nên khoảng cách giữa 2 mặt phẳng là khoảng cách từ M đến mặt phẳng (P₂):

BÀI TẬP

Bài tập 1:  Phương trình nào sau đây là phương trình tổng quát của mặt phẳng?

Trả lời rút gọn:

Phương trình tổng quát của mặt phẳng trong không gian được viết dưới dạng: 

 D.

Bài tập 2: Mặt phẳng x + 2y - 3z + 4 = 0 có một vectơ pháp tuyến là:

A. = (2; -3; 4).

B. = (1; 2; 3).

C. = (1; 2; -3).

D. = (1; 2; 4).

Trả lời rút gọn:

Mặt phẳng x + 2y - 3z + 4 = 0 có một vectơ pháp tuyến là hệ số của x,y,z: 

C.

Bài tập 3: Lập phương trình mặt phẳng (P) đi qua điểm I(3;-4;5) và nhận làm vectơ pháp tuyến.

Trả lời rút gọn:

Phương trình mặt phẳng (P) nhận làm vectơ pháp tuyến có dạng:

Mặt phẳng chứa điểm I(3;-4;5):

(P) :

Bài tập 4: Lập phương trình mặt phẳng (P) đi qua điểm (K(-1;2;3) và nhận hai vectơ và làm cặp vectơ chỉ phương.

Trả lời rút gọn:

Vectơ pháp tuyến của mặt phẳng (P) là:

Phương trình mặt phẳng (P) có dạng:

Mặt phẳng (P) đi qua điểm K(-1;2;3)

(P) :

Bài tập 5: Lập phương trình mặt phẳng (P) đi qua:

a) Điểm I (3; −4; 1) và vuông góc với trục Ox,

b) Điểm K(-2;4;-1) và song song với mặt phẳng (Ozx);

c) Điểm K(-2;4;-1) và song song với mặt phẳng (Q): 3x+7y+10z+1=0.

Trả lời rút gọn:

a) Khi mặt phẳng vuông góc với trục Ox, phương trình của nó có dạng:

x = c

Vì mặt phẳng đi qua điểm I(3, -4, 1), nên phương trình mặt phẳng là:

 x = 3 

b) Khi mặt phẳng song song với mặt phẳng (Ozx), phương trình của nó có dạng:

y = c 

Vì mặt phẳng đi qua điểm K(-2, 4, -1), nên phương trình mặt phẳng là:

 y = 4 

c) Khi mặt phẳng (P) song song với mặt phẳng (Q), phương trình của (P) sẽ có dạng:

Vì mặt phẳng (P) đi qua điểm  K(-2, 4, -1) , ta thay tọa độ điểm (K) vào phương trình mặt phẳng:

Do đó, phương trình mặt phẳng (P) là:

Bài tập 6: Lập phương trình mặt phẳng (P) đi qua ba điểm A(1; 1; 1), B(0; 4; 0), C(2; 2; 0).

Trả lời rút gọn:

Chọn hai vectơ chỉ phương của mặt phẳng (P) là:

Vectơ pháp tuyến của mặt phẳng (P) là:

Chọn điểm A(1; 1; 1) để viết phương trình mặt phẳng (P).

Bài tập 7:  Lập phương trình mặt phẳng theo đoạn chắn của mặt phẳng (P), biết (P) đi qua ba điểm A(5; 0; 0), B(0; 3; 0), C(0; 0; 6).

Trả lời rút gọn:

Phương trình mặt phẳng theo đoạn chắn của mặt phẳng (P), biết (P) đi qua ba điểm A(5; 0; 0), B(0; 3; 0), C(0; 0; 6):

Bài tập 8: Cho hai mặt phẳng

a) Chứng minh rằng

b) Tính khoảng cách giữa hai mặt phẳng song song

Trả lời rút gọn:

a) 

- Vector pháp tuyến của là

- Vector pháp tuyến của là

Xét tỉ lệ giữa các thành phần của 2 vector:

Do đó, hai vector pháp tuyến và là cùng phương. Vì vậy, hai mặt phẳng và là song song.

b) Chọn điểm

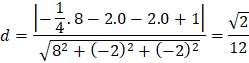
Bài tập 9: a) Cho hai mặt phẳng Chứng minh rằng

b) Cho mặt phẳng và điểm M(1; 1; -6). Tính khoảng cách từ điểm M đến mặt phẳng (P)

Trả lời rút gọn:

a)

Vector pháp tuyến của mặt phẳng (P₁):

Vector pháp tuyến của mặt phẳng (P₂):

Để thì

Vậy  

b) 

Bài tập 10: Trong không gian với hệ toạ độ Oxyz, cho hình chóp S.OBCD có đáy là hình chữ nhật và các điểm O(0;0;0), B(2; 0; 0), D(0; 3; 0), S(0; 0; 4) (Hình 19).

a) Tìm toạ độ điểm C.

b) Viết phương trình mặt phẳng (SBD).

c) Tính khoảng cách từ điểm C đến mặt phẳng (SBD).

Trả lời rút gọn:

a) 

Vậy điểm C(2;3;0)

b) Viết phương trình mặt phẳng (SBD)

Tọa độ điểm B(2;0;0)

Tọa độ điểm D(0;3;0)

Tọa độ điểm S(0;0;4)

Ba điểm S(0, 0, 4), B(2, 0, 0) và D(0, 3, 0) không thẳng hàng nên chúng xác định một mặt phẳng.

Tích có hướng của hai vectơ này là:

Phương trình mặt phẳng có dạng:

Thay tọa độ điểm S(0, 0, 4) vào phương trình trên:

Vậy phương trình mặt phẳng là:

c) 

Tọa độ điểm C là (2, 3, 0). 

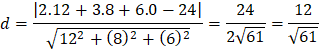
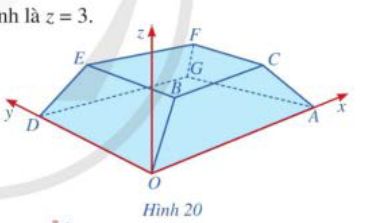
Bài tập 11: Hình 20 minh họa hình ảnh một tòa nhà trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là mét). Biết A(50; 0; 0), D(0; 20; 0), B(4k; 3k; 2k) với k > 0 và mặt phẳng (CBEF) có phương trình là z = 3.

a) Tìm tọa độ của điểm B.

b) Lập phương trình mặt phẳng (AOBC).

c) Lập phương trình mặt phẳng (DOBE).

Trả lời rút gọn:

a)  Mặt phẳng (CBEF) có chứa điểm B có phương trình:

Thay tọa độ điểm B vào, ta có:

b) Mặt phẳng (AOBC) đi qua các điểm A(50; 0; 0), ,O(0,0,0)

Tính vector pháp tuyến:

Phương trình mặt phẳng (AOBC) có dạng

Thay O vào phương trình, ta được:

Phương trình mặt phẳng (AOBC) là:

c) Phương trình mặt phẳng (DOBE) đi qua các điểm D(0; 20; 0), O(0,0,0) và ,

Ta có:

Rút gọn:

Phương trình mặt phẳng (DOBE) có dạng

Thay điểm D vào phương trình, ta được D=0.

Phương trình mặt phẳng (DOBE) có dạng

d) Vector pháp tuyến của mặt phẳng (AOBC): là:

Vector pháp tuyến của mặt phẳng (DOBE): là:

Bài tập 12: Hình 21 minh họa một khu nhà đang xây dựng được gắn hệ trục tọa độ Oxyz (đơn vị trên các trục là mét). Mỗi cột bê tông có dạng hình lăng trụ tứ giác đều và tâm của mặt đáy trên lần lượt là các điểm A(2; 1; 3), B(4; 3; 3), C(6; 3; 2,5), D(4; 0; 2,8).

a) Viết phương trình mặt phẳng (ABC).

b) Bốn điểm A, B, C, D có đồng phẳng không?

Trả lời rút gọn:

Mặt phẳng (ABC) đi qua điểm A(2; 1; 3), B(4; 3; 3), C(6; 3; 2,5).

Tính các vector

Phương trình mặt phẳng ABC có dạng: 

Thay điểm A vào ta có:

Vậy phương trình mặt phẳng (ABC) là::

b) Thay D(4;0;2,8) vào phương trình (ABC), ta có:

Vậy 4 điểm A,B,C,D không thẳng hàng do D không thuộc mặt phẳng (ABC)