Slide bài giảng Toán 12 cánh diều Bài 3: Tích phân

Tóm lược nội dung

TÍCH PHÂN

I. ĐỊNH NGHĨA TÍCH PHÂN 

1. Bài toán dẫn tới khái niệm tích phân 

Hoạt động 1: Cho hàm số . Xét hình phẳng ( được tô màu) gồm tất cả điểm M(x,y) trên mặt phẳng tọa độ sao . Hình phẳng đó gọi là hình thang cong AMNB giới hạn bởi đồ thị của hàm số , trục Ox và đường thẳng x=1, x=2. 

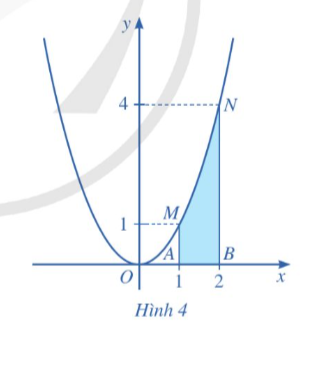
Chia đoạn [1;2] thành n phần bằng nhau bởi các điểm chia:

a) Tính diện tích của hình chữ nhật dựng trên đoạn với chiều cao

Tính diện tích của hình chữ nhật dựng trên đoạn với chiều cao

Tính diện tích của hình chữ nhật dựng trên đoạn với chiều cao

Tính diện tích của hình chữ nhật dựng trên đoạn với chiều cao

b) Đặt Chứng minh rằng:

Trả lời rút gọn:

a) Diện tích của hình chữ nhật dựng trên đoạn với chiều cao :

Tính diện tích của hình chữ nhật dựng trên đoạn với chiều cao

Tính diện tích của hình chữ nhật dựng trên đoạn với chiều cao

Tính diện tích của hình chữ nhật dựng trên đoạn với chiều cao

b) 

Vì các đoạn là bằng nhau và bằng nên ta có 

Vận dụng 1: Cho đồ thị hàm số Xét tam giác vuông OAB giới hạn bởi đồ thị của hàm số , trục Ox và đường thẳng x=2.

a) Tính diện tích tam giác vuông OAB.

b) Giả sử F(x) là 1 nguyên hàm của trên đoạn [0,2]. Chứng tỏ rằng

Trả lời rút gọn:

a)

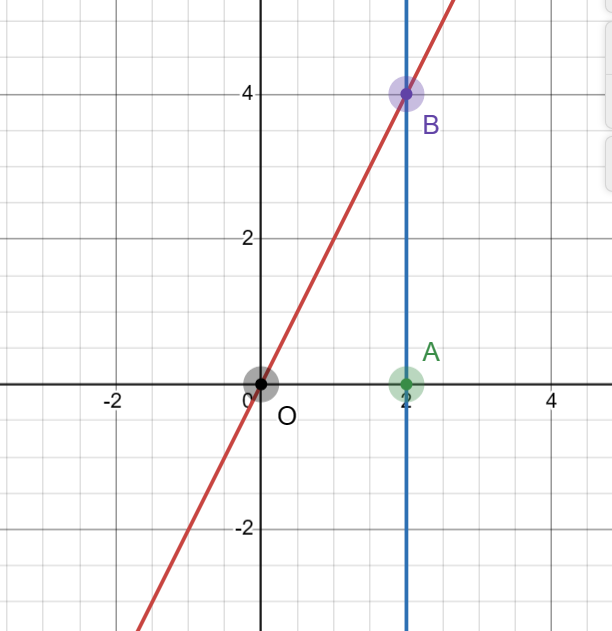
O là gốc tọa độ, O(0,0).

A nằm trên trục Ox, do x=2 nên A(2,0)

B nằm trên điểm giao giữa đồ thị hàm số y=2x và đường x=2, y tại B=4 nên B(2,4)

Diện tích tam giác vuông OAB là:

b)

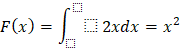
Giá trị vừa tính thỏa mãn giá trị đã tính ở phần a.

2. Định nghĩa tích phân 

Hoạt động 2: Cho hàm số

a) Chứng tỏ rằng là các nguyên hàm của hàm số .

b) Chứng minh rằng , tức là hiệu số không phụ thuộc vào việc chọn nguyên hàm. 

Trả lời rút gọn:

a) 

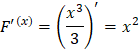
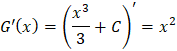
Vậy là các nguyên hàm của hàm số

b)

Vậy hiệu số không phụ thuộc vào việc chọn nguyên hàm. 

Vận dụng 2: Tính

Trả lời rút gọn:

II. TÍNH CHẤT CỦA TÍCH PHÂN

Hoạt động 3: So sánh và :

Trả lời rút gọn:

Vậy =

Vận dụng 3: Cho

Tính

Trả lời rút gọn:

Hoạt động 4: So sánh:

a) và  

b) và

Trả lời rút gọn:

a) 

Vậy =

b) 

Vậy =

Vận dụng 4: Tính

Trả lời rút gọn:

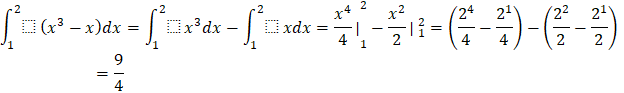
Hoạt động 5: So sánh và :

Trả lời rút gọn:

Vậy =

Vận dụng 5: Tính

Trả lời rút gọn:

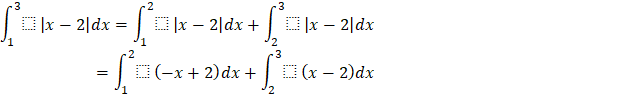
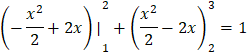
III. TÍCH PHÂN CỦA MỘT SỐ HÀM SỐ SƠ CẤP

1. Tích phân của hàm số lũy thừa

Vận dụng 6: a)

b)

c)

Trả lời rút gọn:

a) 

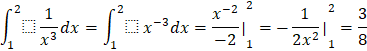
b) 

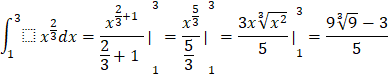
c)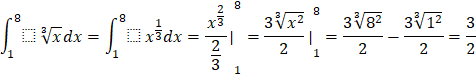

2. Tích phân của hàm số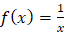

Vận dụng 7: Tính

Trả lời rút gọn:

3. Tích phân của hàm số lượng giác

Vận dụng 8: Tính: 

a)

b)

Trả lời rút gọn:

a) 

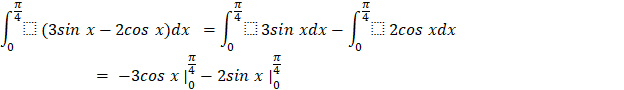
b) 

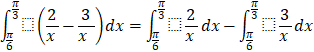
4. Tích phân của hàm số mũ

Vận dụng 9: a)

b)

Trả lời rút gọn:

a)

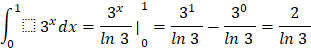
b) 

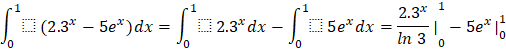
GIẢI BÀI TẬP CUỐI SÁCH GIÁO KHOA

Bài tập 1: Tích phân có giá trị bằng:

A.

B.

C.

D.

Trả lời rút gọn: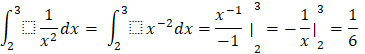

Đáp án A.

Bài tập 2: Tích phân có giá trị bằng:

A.

B.

C.

D.

Trả lời rút gọn:

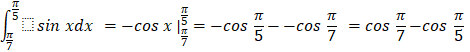
Đáp án D.

Bài tập 3: Tích phân có giá trị bằng:

A.

B.

C. -1

D. 1

Trả lời rút gọn:

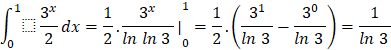
Đáp án B.

Bài tập 4: Cho , F(x) là một nguyên hàm của hàm số f(x) trên đoạn [-2;3], 

F(3) =8. Tính F(-2).

Trả lời rút gọn:

Mà:

Do đó:

Bài tập 5: Cho Tính

Trả lời rút gọn:

Bài tập 6:  Tính:

a)

b)

c)

d)

e)

g)

h)

i)

k)

Trả lời rút gọn:

a)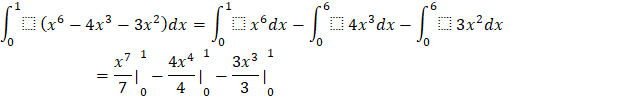

b)

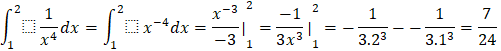
c) 

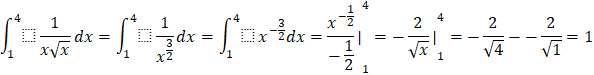
d)

e)

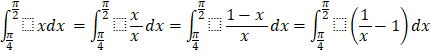
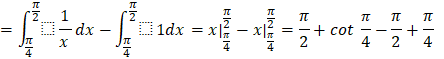
g) 

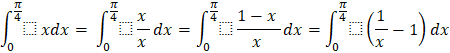
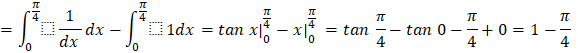
h) 

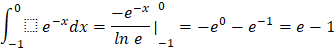
i) 

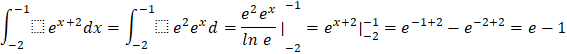
k)

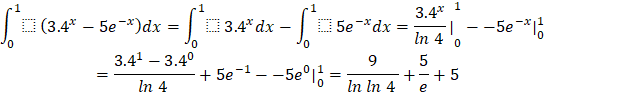
Bài tập 7: a) Cho một vật chuyển động với vận tốc y=v(t) (m/s). Cho 0 < a < b và v(t) > 0 với mọi . Hãy giải thích vì sao biểu thị quãng đường mà vật đi được trong khoảng thời gian từ a đến b(a,b tính theo giây).

b) Áp dụng công thức của câu a) để giải bài toán sau: Một vật chuyển động với vận tốc (m/s). Tính quãng đường vật di chuyển được trong khoảng thời gian từ thời điểm t=0(giây) đến thời điểm (giây).

Trả lời rút gọn:

a)

+ v(t) là vận tốc tức thời là đại lượng cho biết tốc độ và hướng di chuyển của 1 vật tại thời điểm t (m/s).

+ s là tổng chiều dài quãng đường mà vật di chuyển trong khoảng thời gian nhất định, không phụ thuộc vào hướng di chuyển mà chỉ phụ thuộc vào độ lớn của vận tốc.Theo định nghĩa của tích phân, tích phân biển diễn tổng diện tích dưới của đồ thị hàm số v(t) từ t=a đến t=b. 

Vì vận tốc v(t) luôn dương trên [a;b], tích phân chính là tổng của các đoạn đường nhỏ mà vật đã di chuyển đi được từ thời điểm a đến thời điểm b, tức là biểu thị quãng đường vật di chuyển trong khoảng thời gian từ a đến b.

b) Quãng đường vật di chuyển được trong khoảng thời gian từ thời điểm t=0(giây) đến thời điểm (giây) khi (m/s):

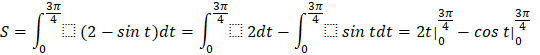
Vậy quãng đường vật di chuyển được trong khoảng thời gian từ thời điểm t=0(giây) đến thời điểm (giây) là  mét.

Bài tập 8: Một vật chuyển động với vận tốc được cho bởi đồ thị ở hình 9.

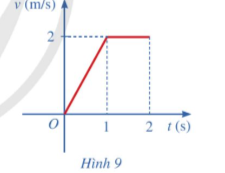
a) Tính quãng đường của vật di chuyển được trong 1 giây đầu tiên. 

b) Tính quãng đường mà vật di chuyển được trong 2 giây đầu tiên.

Trả lời rút gọn:

a) 

Xét t(s) bằng 1, v(t) bằng 2, vì vậy v(t) = 2t

Quãng đường mà vật di chuyển trong 1 giây đầu tiên là tích phân của v(t) trên đoạn [0;1]:

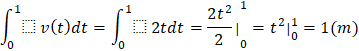
b) 

Xét tại t(s) bằng 1 và t(s) =2, v(t) = 2, vì vậy v(t) =t

Quãng đường mà vật di chuyển trong 2 giây đầu tiên là tích phân của v(t) trên đoạn [0,2]:

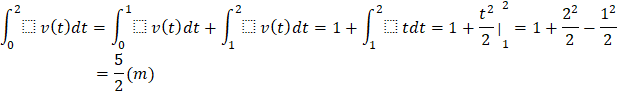
Bài tập 9: Ở nhiệt độ 37 °C, một phản ứng hoá học từ chất đầu A, chuyển hoá thành chất sản phẩm B theo phương trình: A → B. Giả sử y(x) là nồng độ chất A (đơn vị mol L⁻¹) tại thời gian x (giây), y(x) > 0 với x ≥ 0 thoả mãn hệ thức: với x ≥ 0 Biết rằng tại x = 0 nồng độ ban đầu của chất A là 0,05 mol L⁻¹.

a) Xét hàm số với x ≥ 0. Hãy tính f'(x), từ đó hãy tìm hàm số f(x).

b) Giả sử ta tính nồng độ trung bình chất A (đơn vị mol L¯¹) từ thời điểm a (giây) đến thời điểm b (giây) với 0 < a < b theo công thức . Xác định nồng độ trung bình của chất A từ thời điểm 15 giây đến thời điểm 30 giây

Trả lời rút gọn:

a)

Mà theo đề bài:

Thay y’(x) vào biểu thức f’(x), ta có:

Vậy 

Để tìm f(x), ta tính nguyên hàm biểu thức f’(x) vừa tìm được

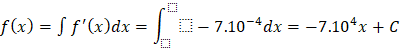
Mà theo đề bài, Tại x=0, y(0) =0,05. Vậy:

Thay x=0 vào hàm f(x):

Do đó:

b)

Để xác định nồng độ trung bình C_A của chất A từ thời điểm a= 15 giây đến thời điểm b= 30 giây, ta sử dụng công thức:

Mà 

Do đó:

Tính tích phân của y(x):

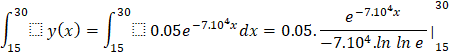
Tính nồng độ C_A:

Vậy, nồng độ trung bình của chất A từ thời điểm 15 giây đến thời điểm 30 giây là khoảng 0.00495 mol/L.