Giải câu 10 bài tập cuối chương IV
Bài tập 10. Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là h = 1,2m. Gọi D là đỉnh tháp và hai điểm $A_{1}$, $B_{1}$ cùng thẳng hàng với $C_{1}$ thuộc chiều cao CD của tháp. Người ta đo được $\widehat{DA_{1}C_{1}} = 49^{\circ}$, $\widehat{DB_{1}C_{1}} = 35^{\circ}$. Tính chiều cao CD của tháp.
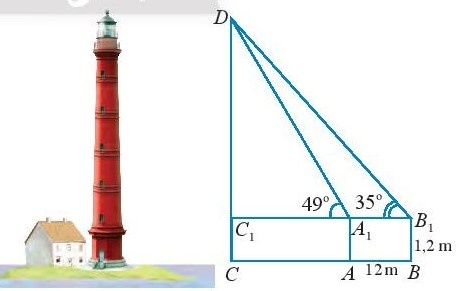
Ta có: $\widehat{B_{1}DA_{1}} = \widehat{C_{1}A_{1}D} - \widehat{A_{1}B_{1}D} = 49^{\circ} - 35^{\circ} = 14^{\circ}$
Áp dụng định lí sin, ta có: $\frac{A_{1}B_{1}}{sin\widehat{B_{1}DA_{1}}} = \frac{DA_{1}}{sin\widehat{A_{1}B_{1}D}}$
$\Rightarrow DA_{1} = \frac{A_{1}B_{1}.sin\widehat{A_{1}B_{1}D}}{sin\widehat{B_{1}DA_{1}}} = \frac{12.sin35^{\circ}}{sin14^{\circ}} \approx$ 28,5 (m)
Xét tam giác $DA_{1}C_{1}$ vuông tại $C_{1}$, ta có: $DC_{1}$ = $DA_{1}.sin\widehat{C_{1}A_{1}D}$ = 28,5. sin$49^{\circ}$ $\approx$ 21,5 (m)
Ta có: DC = $DC_{1} + C_{1}C$ = 21,5 + 1,2 = 22,7 (m)
Vậy ngọn tháp có chiều cao khoảng 22,7 m.
Xem toàn bộ: Giải bài tập cuối chương IV trang 78

Bình luận