Giải câu 1 trang 94 toán VNEN 7 tập 2

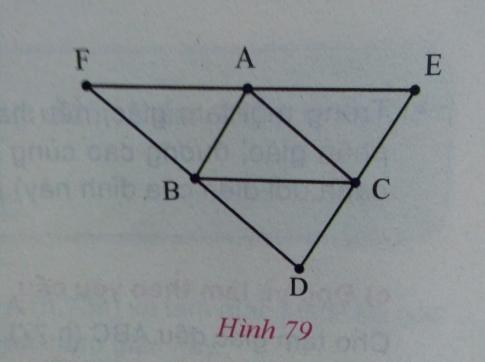
a) Xét tam giác ABC  và tam giác ACE:

- AC là cạnh chung

- $\widehat{ACB}$ = $\widehat{CAE}$ (so le trong, AE //BC)

- $\widehat{CAB}$ = $\widehat{ACE}$ (so le trong, CE //AB)

Do đó: $\Delta ABC$ = $\Delta CEA$ (g.c.g)

=> AE = BC                  (1)

Xét $\Delta ABC$ và $\Delta ABF$ có:

- $\widehat{ABC}$ = $\widehat{BAF}$ (so le trong, BE //AC)

-  $\widehat{BAC}$ = $\widehat{ABF}$ (so le trong, BF //AC)

- AC là cạnh chung

Do đó: $\Delta ABC$ = $\Delta BAF$ (g.c.g)

=> AF = BC                    (2)

Từ (1) và (2) suy ra: AE = AF.

Vậy A là trung điểm của EF.

b) Kẻ AH vuông góc với BC

 EF // BC (gt)

=> AH vuông góc với EF

AE = AF (chứng minh trên)

Vậy đường cao AH là đường trung trực của EF.

Chứng minh tương tự câu a, ta có B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của tam giác ABC là đường trung trực DF.

Ta có C là trung điểm của DE và DE // AB nên đường cao kẻ từ đỉnh C của ∆ABC là đường trung trực của DE.