Giải VNEN toán 7 bài 4: Đa thức
Giải VNEN toán 7 bài 4: Đa thức - Sách hướng dẫn học Toán 7 tập 2 trang 41. Sách này nằm trong bộ VNEN của chương trình mới. Dưới đây sẽ hướng dẫn trả lời và giải các bài tập trong bài học. Cách giải chi tiết, dễ hiểu. Hi vọng các em học sinh nắm tốt kiến thức.
B. Hoạt động hình thành kiến thức
1. a) Thực hiện theo yêu cầu
- Xem hình 4 rồi viết biểu thức đại số biểu thị diện tích của hình tạo bởi một tam giác vuông và hai hình vuông dựng về phía ngoài trên hai cạnh góc vuông x, y của tam giác đó.
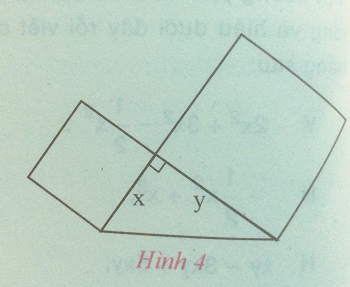
Trả lời:
- Diện tích hình tam giác: $ \frac{1}{2}$xy
- Diện tích hình vuông có cạnh x : x2
- Diện tích hình vuông có cạnh y : y2
=> Diện tích hình 4 là : $ \frac{1}{2}$xy + x2 + y2.
c) Viết một đa thức có hai biến x, y và chỉ rõ các hạng tử của đa thức đó.
Trả lời:
- Đa thức hai biến: 3x2 + 2xy - $\frac{3}{4} $xy2
- Đa thức trên có ba hạng tử là : 3x2 ; 2xy và - $\frac{3}{4} $xy2
2. a) Cho đa thức A = -2x2y3 – xy + 3x2y3 -13 +$\frac{2}{3} $xy - $\frac{1}{7}$x -1.
- Viết các hạng tử của đa thức A.
- Chỉ rõ các đơn thức đồng dạng trong các hạng tử của đa thức A.
- Thực hiện phép cộng các đơn thức đồng dạng của đa thức A.
Trả lời:
Các hạng tử của đa thức A là: -2x2y3 ; – xy ; 3x2y3 ; -13 +; $\frac{2}{3} $xy ; - $\frac{1}{7}$x ; -1.
Các đơn thức đồng dạng trong đa thức A là:
- -2x2y3 và 3x2y3
- – xy và $\frac{2}{3} $xy
- -13 và -1
A = -2x2y3 – xy + 3x2y3 -13 +$\frac{2}{3} $xy - $\frac{1}{7}$x -1
A = (-2x2y3 + 3x2y3) + (– xy + $\frac{2}{3} $xy) - $\frac{1}{7}$x + (-13 -1)
A = x2y - $-\frac{1}{3} $xy - $\frac{1}{7}$x -14
c) Thu gọn đa thức sau
- Q = 7x2y – 2xy + $\frac{1}{2} $x2y –xy + 11xy - $\frac{1}{3} $x + $\frac{1}{3} $ + $\frac{2}{3} $x - $\frac{1}{6} $
Trả lời:
Q = (7x2y + $\frac{1}{2} $x2y) + (– 2xy –xy + 11xy)+ (- $\frac{1}{3} $x + $\frac{2}{3} $x ) + ($\frac{1}{3} $ - $\frac{1}{6} $)
Q = $\frac{15}{2} $x2y +8xy + $\frac{1}{3} $x + $\frac{1}{6} $
3. a) Cho đa thức M = x2y5 – xy4 + y6 + 1
- Viết các hạng tử của đa thức M và chỉ rõ bậc của các hạng tử đó.
- Chỉ rõ bậc cao nhất trong các bậc của các hạng tử của đa thức M.
Trả lời:
- Các hạng tử của đa thức M là:
- x2y5 có bậc là 7
- – xy4 có bậc là 5
- y6 có bậc là 6
- 1 có bậc là 0
- Bậc cao nhất trong các bậc của các hạng tử của đa thức M là 7.
- Bậc của đa thức M là 7
c) Thực hiện theo yêu cầu
- Tìm bậc của đa thức H = -5x6 - $ \frac{1}{2}$x3y - $ \frac{3}{4}$xy2 + 5x6 + 11
- Viết một đa thức có ba biến là x, y, z và có bậc là 6.
Trả lời:
Ta có H = (-5x6 + 5x6) - $ \frac{1}{2}$x3y - $ \frac{3}{4}$xy2 + 11
H = - $ \frac{1}{2}$x3y - $ \frac{3}{4}$xy2 + 11
=> Hạng tử có bậc bao nhất trong đa thức H là - $ \frac{1}{2}$x3y có bậc 4
=> Bậc của đa thức H là 4.
Đa thức có ba biến x, y, z có bậc là 6 là : -2x2y3z – 3z + $\frac{1}{2} $

Bình luận