Giải câu 1 trang 93 toán VNEN 7 tập 2
Câu 1: Trang 93 sách toán VNEN 7 tập 2
a) Cho tam giác ABC có các đường cao BD và CE bằng nhau. Chứng minh rằng tam giác đó là tam giác cân.
b) Cho tam giácABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC
a) 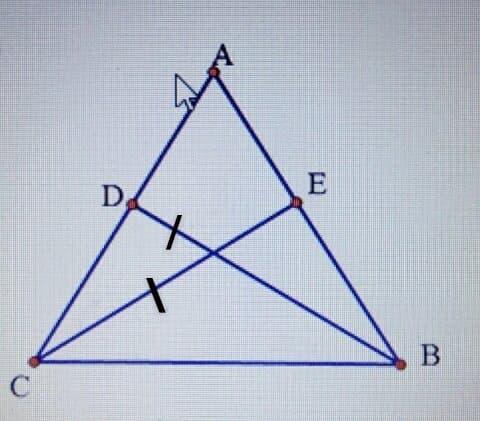
Xét $\Delta DCB$ và $\Delta EBC$, có:
- BC là cạnh chung
- $\widehat{CDB}$ = $\widehat{CEB}$ = $90^{o}$
- BD = CE (gt)
=> $\Delta DCB$ = $\Delta EBC$
=> $\widehat{DCB}$ = $\widehat{EBC}$
hay $\widehat{ACB}$ = $\widehat{ABC}$
=> Tam giác ABC cân.
b) 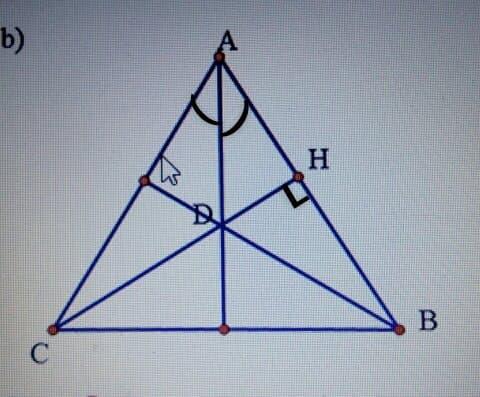
Ta có:
$\Delta ABC$ cân có: AD là tia phân giác của góc A => A cũng là đường cao.
Trong $\Delta ABC$ có 2 đường cao AD và CH cắt nhau tại D
=> D là trực tâm của $\Delta ABC$
=> BD cũng là đường cao của tam giác ABC => BD vuông góc với AC

Bình luận