Giải bài tập 59 trang 86 SBT toán 7 tập 2 cánh diều
Bài 59. Cho tam giác ABC có $\widehat{B}$ và $\widehat{C}$ nhọn. H và K lần lượt là hình chiếu của B và C trên Ax (Hình 41). Chứng minh:
a) BH + CK $\leq $ BC
b) Nếu tổng BH + CK lớn nhất thì tia Ax phải vuông góc với BC.
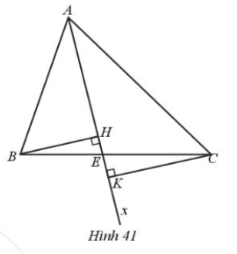
a) Ta có $BH \leq BE;CK\leq CE$ nên $BH + CK\leq BE+CE=BC$
b) Do BH + CK lớn nhất nên BH = BE, CK = CE. Do đó $Ax\perp BC$

Bình luận