Giải bài tập 58 trang 86 SBT toán 7 tập 2 cánh diều
Bài 58. Cho tam giác ABC vuông tại A (AB < AC), BD là tia phân giác của góc ABC (D$\in $AC). Qua C kẻ tia Cx vuông góc với AC cắt BD tại M.
a) Chứng minh tam giác CBM là tam giác cân.
b) So sánh độ dài CM và AC.
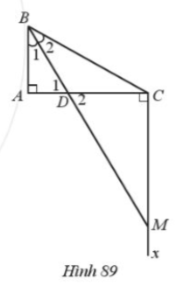
a) Trong tam giác CDM có $\widehat{M}+\widehat{D2}=90^{\circ}$
Trong tam giác ABD có: $\widehat{B1}+\widehat{D1}=90^{\circ}$
$\widehat{B1}=\widehat{B2};\widehat{D1}=\widehat{D2} $ (đối đỉnh)
nên $\widehat{M}=\widehat{B2}$
Suy ra tam giác CBM cân tại C.
b) Tam giác CBM cân tại C => CM =BC mà BC > AC nên CM > CA

Bình luận