Giải bài tập 50 trang 84 SBT toán 7 tập 2 cánh diều
Bài 50. Cho tam giác đều ABC. Gọi E, D, F là ba điểm lần lượt nằm trên ba cạnh AB, AC, BC sao cho AD = CF = BE. Chứng minh tam giác DEF là tam giác đều.
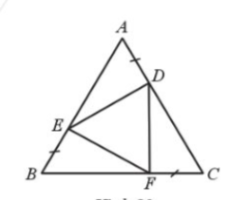
Xét tam giác ADE và BEF ta có:
AD = BE (gt)
$\widehat{DAE}=\widehat{EBF}$ (do tam giác ABC đều)
AE = BF
Suy ra $\Delta ADE=\Delta BEF$ (c.g.c) nên DE = EF (1)
Tương tự $\Delta BEF = \Delta CFD$ (c.g.c) nên EF = FD (2)
Từ (1) (2) suy ra DE = FD = EF.
Vậy tam giác DEF đều.
Xem toàn bộ: Giải SBT toán 7 Cánh diều bài 7 Tam giác cân
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 7 cánh diều
Giải SBT lớp 7 kết nối tri thức
Giải SBT lớp 7 chân trời sáng tạo
Giải SBT lớp 7 cánh diều
Trắc nghiệm 7 Kết nối tri thức
Trắc nghiệm 7 Chân trời sáng tạo
Trắc nghiệm 7 Cánh diêu
Bình luận