Giải bài tập 48 trang 83 SBT toán 7 tập 2 cánh diều
Bài 48. Cho tam giác ABC cân tại A có $\widehat{BAC}=120^{\circ}$. Trên cạnh BC lấy các điểm D, E sao cho BD = BA, CE = CA.
a) Chứng minh các tam giác BAD, CAE, AED là tam giác cân.
b) Tính số đo mỗi góc của tam giác ADE.
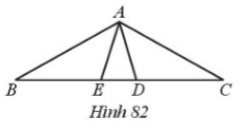
a) Do BA = BD nên tam giác BAD cân tại B, CE = CA nên tam giác CAE cân tại C.
Tam giác ABC cân tại A có $\widehat{BAC}=120^{\circ}$ suy ra $\widehat{ABC}=\widehat{ACB}=30^{\circ}$
Tam giá BAD cân tại B có $\widehat{ABD}=30^{\circ}$ suy ra $\widehat{ADB}=75^{\circ}$.
Tương tự $\widehat{AEC}=75^{\circ}$
Vậy $\widehat{ADE}=\widehat{AED}$ => tam giác AED cân tại A.
b) Tam giác AED cân tại A và $\widehat{ADE}=\widehat{AED}=75^{\circ}$ nên $\widehat{EAD}=30^{\circ}$.
Vậy số đo các góc ADE, AED và EAD của tam giác ADE lần lượt là: $75^{\circ}, 75^{\circ}, 30^{\circ}$
Xem toàn bộ: Giải SBT toán 7 Cánh diều bài 7 Tam giác cân
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 7 cánh diều
Giải SBT lớp 7 kết nối tri thức
Giải SBT lớp 7 chân trời sáng tạo
Giải SBT lớp 7 cánh diều
Trắc nghiệm 7 Kết nối tri thức
Trắc nghiệm 7 Chân trời sáng tạo
Trắc nghiệm 7 Cánh diêu
Bình luận