Giải bài tập 5 trang 74 SBT toán 8 tập 1 cánh diều:
Bài tập 5 trang 74 SBT toán 8 tập 1 cánh diều:
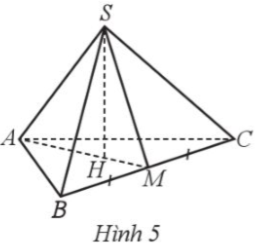
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng 9 cm, SH là chiều cao. Gọi M là trung điểm của BC (Hình 5). Tính thể tích của hình chóp S.ABC, biết H là trọng tâm của tam giác ABC, AH = $\frac{\sqrt{3}}{3}$AB và SH = 2AH.
Ta có: AH = $\frac{\sqrt{3}}{3}$AB nên AH = 3$\sqrt{3}$ cm.
=> SH = 2AH = 6$\sqrt{3}$ cm.
Do H là trọng tâm của tam giác ABC nên AH = $\frac{2}{3}$AM.
=> AM = $\frac{3}{2}$AH = $\frac{3}{2}$.3$\sqrt{3}$ = $\frac{9\sqrt{3}}{2}$ cm.
Ta có: ∆ABM = ∆ACM (c.c.c) => $\widehat{AMB}=\widehat{AMC}$ = 90°.
Do đó AB ⊥ BC.
Diện tích đáy của hình chóp tam giác đều đó là:
$S_{ABC}=\frac{1}{2}.BC.AM=\frac{1}{2}.9.\frac{9\sqrt{3}}{2}=\frac{81\sqrt{3}}{4}$ (cm2).
Thể tích của hình chóp tam giác đều đó là:
$\frac{1}{3}.S_{ABC}.SH=\frac{1}{2}.\frac{81\sqrt{3}}{4}.6\sqrt{3}=\frac{243}{2}$ (cm3).

Bình luận