Giải bài tập 4.9 trang 50 SBT toán 8 tập 1 kết nối:

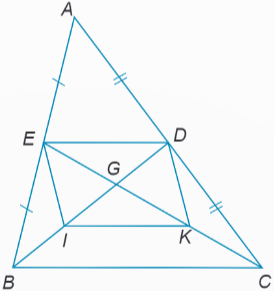
Xét ∆ABC có: E là trung điểm AB; D là trung điểm AC nên DE là đường trung bình của ∆ABC.

Suy ra $ED=\frac{1}{2}BC$ và ED // BC (tính chất đường trung bình của tam giác).

Xét ∆GBC có: I là trung điểm GB; K là trung điểm GC nên IK là đường trung bình của ∆GBC.

Suy ra $IK=\frac{1}{2}BC$ và IK // BC (tính chất đường trung bình của tam giác)

Ta có: ED // BC và IK // BC nên ED // IK.

$ED=\frac{1}{2}BC$ ; $IK=\frac{1}{2}BC$ nên ED = IK.

Xét tứ giác EDKI có ED // IK và ED = IK nên tứ giác EDKI là hình bình hành

Suy ra EI = DK.