Giải bài tập 3.29 trang 44 SBT toán 8 tập 1 kết nối:
Bài tập 3.29 trang 44 SBT toán 8 tập 1 kết nối:
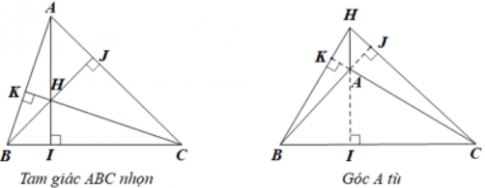
Gọi H là giao của ba đường cao AI, BJ, CK của tam giác nhọn ABC. Dùng công thức tính diện tích tam giác để chứng minh:
$\frac{HI}{AI}=\frac{HJ}{BJ}=\frac{HK}{CK}=1$
Hỏi khi góc A của tam giác ABC là góc tù thì công thức đó thay đổi thế nào?
a) Ta có NM // AC hay MN // AP (do P ∈ BC)
MP // AB hay MP // AN (do N ∈ AB)
Tứ giác ANMP có MN // AP và MP // AN nên là hình bình hành.
b) Để ANMP là hình thoi thì tia AM phải là tia phân giác của góc A.
c) Để ANMP là hình chữ nhật thì hình bình hành ANMP phải có 1 góc vuông.
Khi đó thì góc A phải vuông tức là tam giác ABC vuông tại A.
d) Khi góc A là góc vuông, ANMP là hình chữ nhật nên AM = NP.
Vậy NP ngắn nhất khi AM ngắn nhất, lúc này AM là đường cao của tam giác ABC.
e) Tứ giác ANMP là hình vuông thì nó phải là hình chữ nhật và là hình thoi tức là tam giác ABC vuông tại A và có tia AM là phân giác của góc A.
Xem toàn bộ: Giải SBT Toán 8 Kết nối bài Bài tập cuối chương III

Bình luận