Giải bài tập 3.11 trang 39 SBT toán 10 tập 1 cánh diều
Bài tập 3.11. Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng $N80^{o}E$ với vận tốc 20 km/h. Sau khi đi được 30 phút, tàu chuyển sang hướng $E20^{o}S$ giữ nguyên vận tốc và chạy tiếp 36 phút nữa đến đảo Cát Bà. Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu kilômet?
Trả lời:
Coi điểm xuất phát là A, điểm tàu chuyển hướng là B và đích đến là C
Theo giả thuyết ta có: $\widehat{ABC} = 180^{o} - 10^{o} + 20^{o} = 150^{o}$
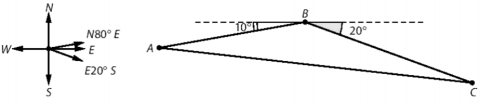
Do tàu chạy từ A tới B với vận tốc 20km/h trong 30 phút nên: AB = 20. $\frac{30}{60}$ = 10 (km)
Do tàu chạy từ B tới C với vận tốc 20km/h trong 36 phút nên: AB = 20. $\frac{36}{60}$ = 12 (km)
Áp dụng định lí côsin cho tam giác ABC ta được:
$AC^{2} = AB^{2} + BC^{2} - 2.AB.BC.cos\widehat{ABC}$
$AC^{2} = 10^{2} + 12^{2} - 2.10.12.cos150$
$AC^{2} \approx 452$
AC $\approx$ 21 (km)

Bình luận