Giải chi tiết bài 13 trang 129 sgk toán 9 tập 2 kntt
Giải chi tiết bài 13 trang 129 sgk toán 9 tập 2 kntt
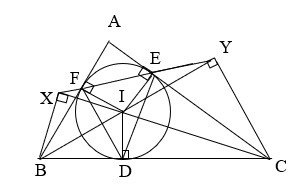
Cho tam giác ABC (AB < AC) ngoại tiếp đường tròn (I) với các tiếp điểm BC, CA, AB lần lượt là D, E, F. Gọi X và Y lần lượt là chân đường cao kẻ từ B và C xuống CI và BI. Chứng minh rằng:
a) DBXF, DCYE là các tứ giác nội tiếp.
b) Bốn điểm X, Y, E, F thẳng hàng.
a) - Xét tứ giác BFID có: ![]() mà hai góc này ở vị trí đối diện nhau
mà hai góc này ở vị trí đối diện nhau
![]() Tứ giác BFID nội tiếp đường tròn đường kính BI (1).
Tứ giác BFID nội tiếp đường tròn đường kính BI (1).
- Xét tứ giác BXFI có ![]() (giả thiết) mà hai góc này kề nhau, cùng nhìn xuống cạnh BI
(giả thiết) mà hai góc này kề nhau, cùng nhìn xuống cạnh BI ![]() Tứ giác BXFI nội tiếp đường tròn đường kính BI (2).
Tứ giác BXFI nội tiếp đường tròn đường kính BI (2).
Từ (1) và (2) ![]() 5 điểm B, F, I, D, F đều nằm trên đường tròn đường kính BI.
5 điểm B, F, I, D, F đều nằm trên đường tròn đường kính BI.
![]() Tứ giác DBXF nội tiếp đường tròn đường kính BI.
Tứ giác DBXF nội tiếp đường tròn đường kính BI.
Chứng minh tương tự:
- Xét tứ giác IECD có: ![]() mà hai góc này ở vị trí đối diện nhau
mà hai góc này ở vị trí đối diện nhau
![]() Tứ giác IECD nội tiếp đường tròn đường kính IC (3).
Tứ giác IECD nội tiếp đường tròn đường kính IC (3).
- Xét tứ giác IEYC có ![]() (giả thiết) mà hai góc này kề nhau, cùng nhìn xuống cạnh IC
(giả thiết) mà hai góc này kề nhau, cùng nhìn xuống cạnh IC ![]() Tứ giác IEYC nội tiếp đường tròn đường kính IC (4).
Tứ giác IEYC nội tiếp đường tròn đường kính IC (4).
Từ (3) và (4) ![]() 5 điểm I, E, C, D, Y đều nằm trên đường tròn đường kính IC.
5 điểm I, E, C, D, Y đều nằm trên đường tròn đường kính IC.
![]() Tứ giác DCYE nội tiếp đường tròn đường kính IC.
Tứ giác DCYE nội tiếp đường tròn đường kính IC.
b) - Ta có: ![]() (giả thiết)
(giả thiết)
![]() (giả thiết)
(giả thiết)
![]()
Mà ![]() (hai góc nội tiếp cùng chắn cunh YC của đường tròn đường kính IC)
(hai góc nội tiếp cùng chắn cunh YC của đường tròn đường kính IC) ![]() .
.
Ta có: AE = AF (AE và AF là hai tiếp tuyến của đường tròn tâm I)
![]() Tam giác AEF cân tại A
Tam giác AEF cân tại A ![]() .
.
Có: ![]() hay
hay ![]() .
.
![]() Y, E, F thẳng hàng (5).
Y, E, F thẳng hàng (5).
Tương tự, ![]() .
.
Mà ![]() (hai góc nội tiếp cùng chắn cunh XB của đường tròn đường kính IB)
(hai góc nội tiếp cùng chắn cunh XB của đường tròn đường kính IB) ![]() .
.
Ta có: ![]() hay
hay ![]() .
.
![]() X, E, F thẳng hàng (6).
X, E, F thẳng hàng (6).
Từ (5) và (6) ![]() Bốn điểm X, Y, E, F thẳng hàng.
Bốn điểm X, Y, E, F thẳng hàng.
Xem toàn bộ: Giải Toán 9 Kết nối Bài tập ôn tập cuối năm
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận