Câu hỏi tự luận mức độ vận dụng Toán 9 cd bài 3: Tiếp tuyến của đường tròn

01 Đề bài:

3. VẬN DỤNG (7 câu)

Câu 1: Cho nửa đường tròn tâm đường kính và là điểm nằm trên . Tiếp tuyến tại cắt tiếp tuyến tại và của lần lượt ở và . Đường thẳng cắt tại , đường thẳng cắt tại .

a) Chứng minh .

b)  Tứ giác là hình gì?

c)  Chứng minh là tiếp tuyến của đường tròn đường kính .

Câu 2: Cho nửa đường tròn tâm đường kính . Một đường thẳng tiếp xúc với đường tròn tại . Gọi và lần lượt là hình chiếu của và trên . Chứng minh rằng:

a) là trung điểm của .

b) Tổng không đổi khi di động trên nửa đường tròn.

c) Tích .

Câu 3: Cho đường tròn đường kính . Lấy thuộc sao cho . Vẽ dây vuông góc với tại . Đường thẳng cắt tại . Đường thẳng qua vuông góc với tại và cắt tại .

a)  Chứng minh cùng thuộc 1 đường tròn.

b)  Chứng minh là tia phân giác của .

c) Chứng minh cân và là tiếp tuyến của .

d) Tìm vị trí của trên để tứ giác trở thành hình thoi.

Câu 4: Cho đường tròn đường kính , vẽ  tại trung điểm của . Các tiếp tuyến với đường tròn tại và cắt nhau ở .

a) Chứng minh rằng thẳng hàng.

b) Tứ giác là hình gì ?

c) Tính .

d) Chứng minh đường thẳng là tiếp tuyến của đường tròn .

Câu 5: Cho vuông tại , là đường cao, . Gọi là điểm đối xứng với qua . Vẽ đường tròn đường kính cắt ở .

a) Chứng minh rằng là tiếp tuyến của đường tròn.

b) Tính độ dài đoạn thẳng .

Câu 6: Cho tam giác cân tại . Vẽ đường tròn tâm đường kính cắt và lần lượt ở và . Gọi là giao điểm của và . Chứng minh rằng :

a) cùng thuộc 1 đường tròn.

b) là tiếp tuyến của đường tròn ở câu .

Câu 7: Cho tam giác cân tại nội tiếp đường tròn tâm . Vẽ hình bình hành , tiếp tuyến tại của đường tròn cắt đường thẳng tại . Chứng minh rằng :

a) Đường thẳng là tiếp tuyến của đường tròn .

b) đồng quy.

02 Bài giải:

Câu 1: 

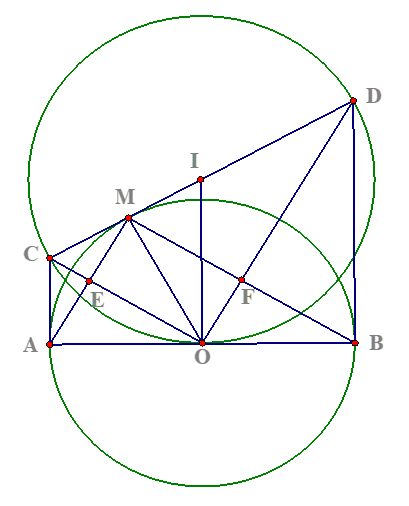
a)  Dễ thấy

Có là các tiếp tuyến

Tương tự ta có:

là phân giác của  

Tương tự là phân giác

b)  Do cân tại nên là đường phân giác đồng thời là đường cao

Tương tự là hình chữ nhật. 

c)  Gọi là trung điểm của thì là tâm đường tròn đường kính và . Có là hình thang vuông tại và nên . Do đó là tiếp tuyến của đường tròn đường kính

Câu 2: 

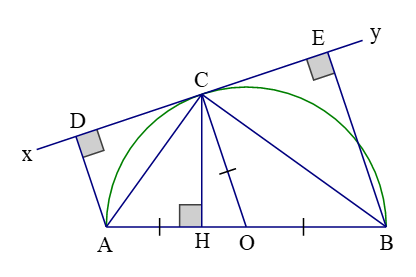
a) Nối ta được

Ta có:

Mặt khác

b) Kẻ

Xét hai tam giác vuông và có:

+)

+)

Chứng minh được:

Điểm nằm trên nửa đường tròn đường kính nên vuông tại

Vậy

Từ đpcm.

Câu 3: 

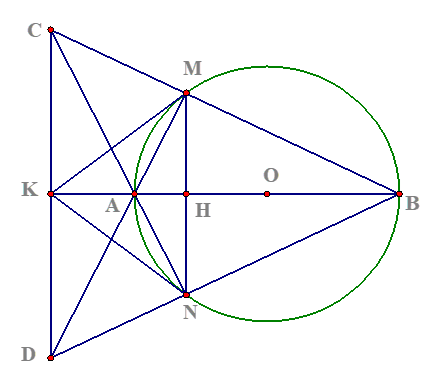
a)  Ta có:

b)  cân tại có là đường cao, trung tuyến và phân giác

c) có là trực tâm thẳng hàng

Ta có vuông tại có là trung tuyến nên cân tại

Lại có:  

Mà là bán kính nên là tiếp tuyến của đường tròn

d)  là hình thoi đều

Câu 4: 

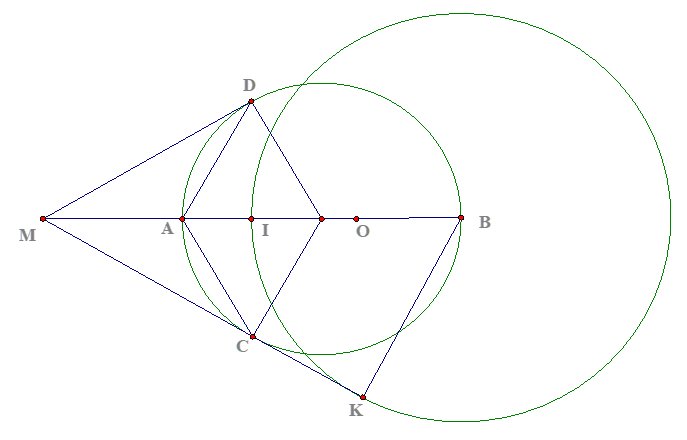
a) là trung trực của , có (tính chất tiếp tuyến) thuộc đường trung trực của thẳng hàng

b) Tứ giác có hai đường chéo vuông góc tại trung điểm mỗi đường nên là hình thoi

c) có nên là tam giác đều

d) Hạ vuông góc , ta có: là phân giác

là phân giác của đpcm

(dựa vào tính chất hai tia phân giác của hai góc kề bù thì vuông góc với nhau)

Ta có: là hai góc kề bù, là phân giác

là phân giác d. là hình thoi đều

Câu 5: 

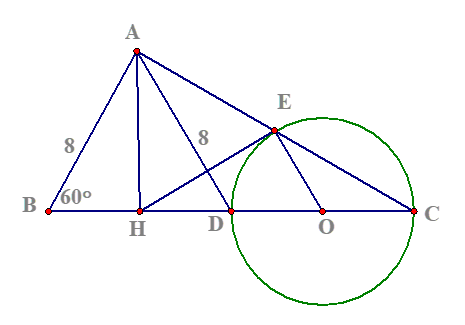
a. Xét

Xét có là đường cao đồng thời là đường trung tuyến nên cân tại , là tam giác đều.

+) Ta có cân tại O

Có: đều

là tiếp tuyến của đường tròn đường kính .

b. Xét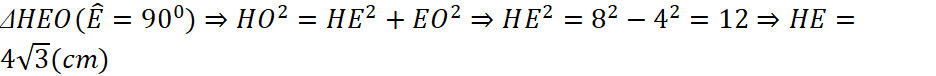

Câu 6: 

a) Ta có là tâm đường tròn đường kính 

vuông.

+) Gọi là trung điểm của

Vậy 4 điểm cùng thuộc 1 đường tròn

b) Có là trực tâm là đường trung trực của thẳng hàng

Mà

là tiếp tuyến (đpcm) 

Câu 7: 

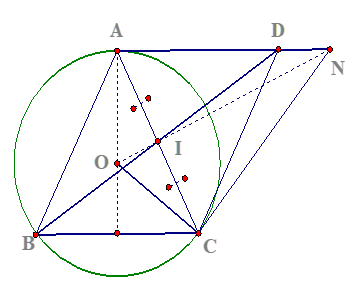
a) Ta có cân tại

Vì tứ giác là hình bình hành

 

Từ đpcm

b) Gọi là giao điểm của và là trung điểm của ( là tiếp tuyến) đồng quy (đpcm).