Câu hỏi tự luận mức độ vận dụng cao Toán 9 Kntt bài 21: Giải bài toán bằng cách lập phương trình

Câu 1: 

a) Giả sử trên mặt phẳng tọa độ, độ dài các đoạn thẳng được tính theo đơn vị mét. Do khoảng cách giữa hai chân cổng là 4 m nên MA = NA = 2m.

Theo giả thiết ta có OM = ON =  

Áp dụng định lý Pythagore ta tính được: OA = 4 vậy M(2; - 4), N(- 2; - 4)

Do M(2; -4) thuộc parabol nên tọa độ điểm M thỏa mãn phương trình: (P): y = a.x² hay -4 = a.2² = a = -1 và (P): y = -x² .

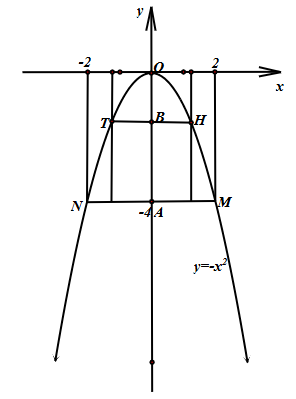
b) Để đáp ứng chiều cao trước hết xe tải phải đi vào chính giữa cổng.

Xét đường thẳng (ứng với chiều cao của xe). Đường thẳng này cắt Parabol tại 2 điểm có tọa độ thỏa mãn hệ:

suy ra tọa độ hai giao điểm là .

Vậy xe tài có thể đi qua cổng.

Câu 2: 

Vẽ đồ thị hàm số y = 2x²

Ta có bảng giá trị: 

Đồ thị y = 2x² như sau: 

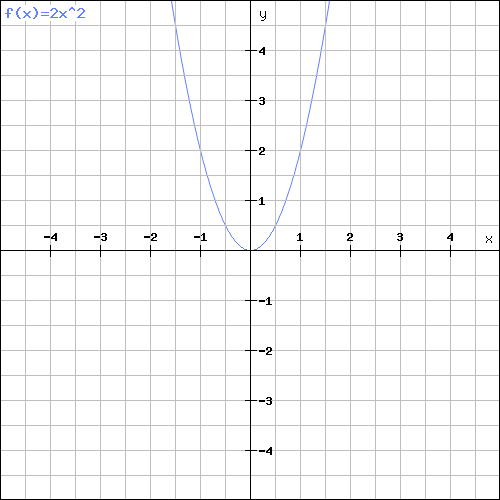
a) Ta thấy, trong đoạn [-4; -2], giá trị của y cao nhất khi x = -4. Vậy giá trị lớn nhất của hàm số trên đoạn [-4; -2] là 32. 

b) Ta thấy, trong đoạn [1;3], giá trị của y lớn nhất khi x = 3 và nhỏ nhất khi x = 1. 

Vậy giá trị của y lớn nhất khi x = 3 <=> y = 18 

giá trị của y nhỏ nhất khi x = 1 <=> y = 2