Câu hỏi tự luận mức độ vận dụng cao Toán 9 kntt bài 20: Định lí Viète và ứng dụng

Câu 1:

Xét phương trình x² – 2mx + 4m – 4 = 0

Phương trình đã cho có hai nghiệm phân biệt khi :

=> m² – 4m + 4 > 0

(m – 2)² > 0

m – 2 0

m 2

Do đó với m 2 thì phương trình đã cho luôn có hai nghiệm phân biệt x₁, x₂.

Áp dụng định lý viète ta có : x₁ + x₂ = 2m và x₁.x₂ = 4m – 4.

Theo đề bài ta có :

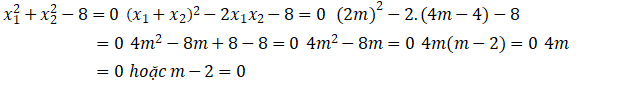
(thỏa mãn điều kiện) hoặc (không thỏa mãn điều kiện) Vậy .

Câu 2: 

a) Giải phương trình (1) khi .

+) Khi , phương trình đã cho trở thành: .

+) Ta có: nên phương trình có hai nghiệm là và .

Vậy khi thì phương trình (1) có hai nghiệm là và .

b) Tìm các giá trị của để phương trình (1) có nghiệm.

+) Ta có: .

+) Để phương trình (1) có nghiệm khi và chỉ khi: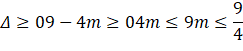

Vậy khi thì phương trình (1) có nghiệm.
c) Tìm các giá trị của m để phương trình (1) có nghiệm thỏa mãn đẳng thức:

+) Theo câu b) phương trình (1) có nghiệm khi (*).
Khi đó theo định lý Viète, ta có: .
Ta có:

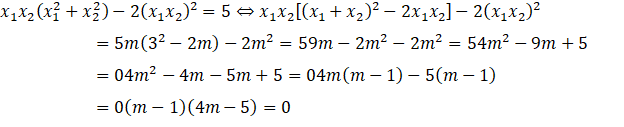
Do đó .

Đối chiếu với điều kiện  (*) ta được các giá trị cần tìm của m là : .