BÀI 1: KHÁI NIỆM PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

I. MỤC TIÊU CẦN ĐẠT CỦA BÀI HỌC

- Nhận biết phương trình, hệ hai phương trình bậc nhất hai ẩn.

- Nhận biết được nghiệm của phương trình và hệ hai phương trình bậc nhất hai ẩn.

- Viết được nghiệm và biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn.

II. NHỮNG NỘI DUNG CẦN GHI NHỚ TRONG BÀI HỌC

1. PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

- Phương trình bậc nhất 2 ẩn x và y là phương trình có dạng: ax + by = c (1) trong đó a, b, c là các số thực; a và b không đồng thời bằng 0

- Cặp số (x₀ ; y₀) gọi là nghiệm của (1) nếu khi thay x = x₀ và y = y₀ thì (1) đúng

- Phương trình (1) luôn có vô số nghiệm và công thức nghiệm tổng quát là

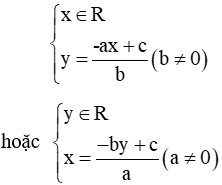
- Nhận xét: Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ (x;y) thỏa mãn phương trình bậc nhất hai ẩn ax + by = c là một đường thẳng. Đường thẳng đó gọi là đường thẳng ax + by = c.

2. HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

1. Một cặp gồm hai phương trình bậc nhất hai ẩn và được gọi là một hệ hai phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng:

(*)

2. Mỗi cặp số được gọi là một nghiệm của hệ (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*). 

Chú ý: Mỗi nghiệm của hệ (*) chính là một nghiệm chung của hai phương trình của hệ (*).

Cách giải hệ phương trình bậc nhất hai ẩn:

+ Bước 1: Từ một phương trình của hệ đã cho (coi là phương trình thức nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn).

+ Bước 2: Dùng phương trình mới ấy để thay thế cho phương trình thức hai trong hệ (phương trình thứ nhất cũng thường được thay thế bởi hệ thức biểu diễn một ẩn theo ẩn kia có được ở bước 1).

+ Bước 3: Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ đã cho.

+ Bước 4: Kết luận.