CHƯƠNG 2

BÀI 1: VECTƠ VÀ CÁC PHÉP TOÁN VECTƠ TRONG KHÔNG GIAN

A. MỤC TIÊU CẦN ĐẠT CỦA BÀI HỌC

- Nhận biết khái niệm vectơ trong không gian và các khái niệm liên quan đến vectơ như: giá của vectơ, độ dài của vectơ, vectơ cùng phương, vectơ cùng hướng, vectơ – không, hai vectơ bằng nhau, hai vectơ đối nhau,...

- Phát biểu và vận dụng được các phép toán tổng và hiệu của hai vectơ trong không gian.

- Nhận biết tích của một số với một vectơ trong không gian.

- Nhận biết, tính được tích vô hướng của hai vectơ trong không gian.

- Vận dụng khái niệm vectơ, các phép toán vectơ trong không gian trong các bài toán thực tế.

B. NHỮNG NỘI DUNG CẦN GHI NHỚ TRONG BÀI HỌC

I. KHÁI NIỆM VECTƠ TRONG KHÔNG GIAN

Vectơ trong không gian là một đoạn thẳng có hướng.

- Cho đoạn thẳng AB trong không gian. Nếu ta chọn điểm đầu là , điểm cuối là thì ta có một vectơ, kí hiệu là , đọc là "vectơ ".

- Khi không cần chỉ rõ điểm đầu và điểm cuối của vectơ, vectơ còn được kí hiệu là ...

Các khái niệm có liên quan đến vectơ trong không gian như: giá của vectơ, độ dài của vectơ, vectơ cùng phương, vectơ cùng hướng, vectơ-không, hai vectơ bằng nhau, hai vectơ đối nhau, ... được định nghĩa tương tự như trong mặt phẳng.

II. CÁC PHÉP TOÁN VECTƠ TRONG KHÔNG GIAN

1. Tổng và hiệu của hai vectơ trong không gian

Trong không gian, cho hai vectơ . Lấy một điểm tuỳ ý, vẽ . Vectơ được gọi là tổng của hai vectơ và , kí hiệu là .

Chú ý:

- Phép lấy tổng của hai vectơ còn được gọi là phép cộng vectơ.

- Phép cộng vectơ trong không gian cũng có các tính chất như phép cộng vectơ trong mặt phẳng, chẳng hạn: Phép cộng vectơ trong không gian cũng có các tính chất giao hoán kết hợp, cộng với vectơ-không.

- Khi thực hiện phép cộng vectơ trong không gian, ta vẫn có thể áp dụng quy tắc ba điểm, quy tắc hình bình hành như đối với vectơ trong mặt phẳng.

Đối với vectơ trong không gian, ta cũng có các quy tắc sau:

• Với ba điểm 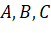trong không gian, ta có: 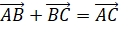(Quy tắc ba điểm);
• Nếu 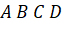là hình bình hành thì 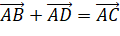(Quy tắc hình bình hành).

- Nếu ABCD.A’B’C’D’ là hình hộp thì (Quy tắc hình hộp)

- Trong không gian, cho hai vectơ . Hiệu của vectơ và vectơ là tổng của vectơ và vectơ đối của vectơ , kí hiệu là

2. Tích của một số với một vectơ trong không gian

Cho số thực và vecto . Tích của một số với vecto là một vectơ, ký hiệu là , được xác định như sau:

Cùng hướng với vectơ nếu , ngược hướng với vectơ nếu ;

Có độ dài bằng .

Trong không gian, cho hai vectơ khác . Lấy một điểm tuỳ ý và vẽ hai vectơ , Góc giữa hai vectơ trong không gian, kí hiệu , là góc giữa hai vectơ .

3. Tích vô hướng của hai vecto trong không gian

- Trong không gian, cho hai vectơ khác . Tích vô hướng của hai vectơ và , kí hiệu , là một số thực được xác định bởi công thức: , ở đó là góc giữa hai vectơ .

-  Trong không gian, cho hai vectơ khác . Tích vô hướng của hai vectơ và kí hiệu , là một số thực được xác định bởi công thức: . = |..cos ở đó là góc giữa hai vectơ .