CHƯƠNG VI. THỐNG KÊ

BÀI 3. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ DỮ LIỆU

1. SỐ TRUNG BÌNH 

HĐKP1:

- Điểm trung bình của Tổ 1 là: $\frac{1}{6}$ (6 + 10 + 6 + 8 + 7 + 10) $\approx $  7,83

- Điểm trung bình của Tổ 2 là: $\frac{1}{6}$ (10 + 6 + 9 + 9 + 8 + 9) = 8,5

Vậy kết quả kiểm tra của Tổ 2 tốt hơn.

Kết luận:

• Giả sử ta có một mẫu số liệu là x$_{1}$, x$_{2}$, x$_{3}$,... x$_{n}$.

Số trung bình (số trung bình cộng) của mẫu số liệu này, kí hiệu là $\bar{x}$, được tính bởi công thức:

$\bar{x}$=$\frac{x_{1}+x_{2}+…+x_{n}}{n}$

• Giả sử mẫu số liệu được cho dưới dạng bảng tần số

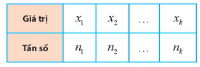
Khi đó, công thức tính số trung bình trở thành:

$\bar{x}$= $\frac{n_{1}x_{1}+n_{2}x_{2}+…+n_{k}x_{k}}{n}$

Trong đó n = n$_{1}$+ n$_{2}$ + ...+ n$_{k}$. Ta gọi n là cỡ mẫu.

Chú ý:

Nếu kí hiệu f$_{k}$=$\frac{n_{k}}{n}$ là tần số tương đối (tần suất) của x$_{k}$ trong mẫu số liệu thì số trung bình còn có thể biểu diễn là:

$\bar{x}$ = f$_{1}$.x$_{1}$ + f$_{2}$.x$_{2}$ + ... + f$_{k}$.x$_{k}$

Ví dụ 1: SGK-tr113

Ý nghĩa của số trung bình:

Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đo xu thế trung tâm của mẫu đó.

Vận dụng 1.

- Số giây trung bình nhóm A chạy được là:

$\frac{1}{8}$ (12,2 + 13,5 + 12,7 + 13,1 + 12,5 + 12,9 + 13,2 + 12,8) = 12,8625 (s)

- Số giây trung bình nhóm B chạy được là: 

$\frac{1}{5}$ (12,1 + 13,4 + 13,2 + 12,9 + 13,7) = 13,06 (s)

Vậy nhóm A có thành tích chạy tốt hơn.

Vận dụng 2.

- Số bàn thắng trung bình đội đó ghi được trong một trận đấu của mùa giải là: 

$\frac{0+1+2+3+4+6}{5+10+5+3+2+1} \approx $ 0,62 (bàn thắng).

2. TRUNG VỊ VÀ TỨ PHÂN VỊ

HĐKP2.

a) Trung bình mỗi bạn Tổ 1 đọc được: 

$\frac{3+1+2+1+2+2+3+25+1}{9} \approx $ 4,44(quyển sách)

Trung bình mỗi bạn Tổ 2 đọc được:

$\frac{4+5+4+3+3+4+5+4}{8}$ = 4

b) Các bạn ở Tổ 2 đọc nhiều sách hơn các bạn ở Tổ 1.

⇒ Kết luận:

Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:

x$_{1} \leq $x$_{2}$ … $\leq $ x$_{n}$

Trung vị của mẫu, kí hiệu là M$_{e}$, là giá trị ở chính giữa dãy x$_{1}$,x$_{2}$,...,x$_{n}$ . Cụ thể:

• Nếu n = 2k + 1, k ∈ N thì trung vị của mẫu M$_{e}$ = x$_{k+1}$

• Nếu n = 2k, k ∈ N thì trung vị của mẫu M$_{e}$ = $\frac{1}{2}$.(x$_{k}$ +x$_{k+1}$).

Ý nghĩa của trung vị:

Trung vị được dùng để đo xu thế trung tâm của mẫu số liệu. Trung vị là giá trị nằm ở chính giữa của mẫu số liệu theo nghĩa: luôn có ít nhất 50% số liệu trong mẫu nhỏ hơn hoặc bằng trung vị.  Khi trong mẫu xuất hiện thêm một giá tri rất lớn hoặc rất nhỏ thì số trung bình sẽ bị thay đổi đáng kể những trung vị thì ít thay đổi.

Ví dụ 2: SGK-tr115

Ví dụ 3: SGK-tr115

Thực hành 1. 

Sắp xếp số giây các bạn nhóm A chạy được theo thứ tự không giảm, ta được dãy: 

12,2; 12,5; 12,7; 12,8; 12,9; 13,1; 13,2; 13,5

Vì cỡ mẫu bằng 8 nên trung vị của nhóm A là trung bình cộng của số liệu thứ 4 và thứ 5 của dãy trên. Vậy M$_{e}$ = $\frac{1}{2}$ (12,8 + 12,9) = 12,85

Sắp xếp số giây các bạn nhóm A chạy được theo thứ tự không giảm, ta được dãy: 12,1; 12,9; 13,2; 13,4; 13,7.

Vì cỡ mẫu bằng 5 nên trung vị của nhóm B là số liệu thứ 3 của dãy trên. Vậy M$_{e}$ = 13,2.

Cỡ mẫu bằng 26. Khi sắp xếp số bàn thắng theo thứ tự không giảm thì số liệu thứ 13 và 14 là 1; 1. Vậy M$_{e}$ = $\frac{1}{2}$(1+1) = 1.

HĐKP3

Sắp xếp số cân nặng theo thứ tự không giảm, ta được dãy:

50; 52; 52; 54; 54; 56; 56; 57; 58; 58; 59; 61; 61; 62; 64; 65; 66; 67; 68; 69

Vì cỡ mẫu là n = 20, là số chẵn, nên giá trị tứ phân vị thứ hai là  

Q$_{2}$= $\frac{1}{2}$(58 + 59) = 58,5.

Tứ phân vị thứ nhất là trung vị của mẫu: 50; 52; 52; 54; 54; 56; 56; 57; 58; 58. Do đó, Q$_{1}$=$\frac{1}{2}$(54 + 56) = 55.

Tứ phân vị thứ ba là trung vị của mẫu: 59; 61; 61; 62; 64; 65; 66; 67; 68; 69. Do đó,

Q$_{3}$=$\frac{1}{2}$(64 + 65) = 64,5

Vậy các ngưỡng cân nặng để huấn luyện viên phân nhóm vận động viên là: 55; 58,5 và 64,5.

Kết luận:

Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:

x$_{1}\leq $ x$_{2}\leq $ … x$_{n}$

Tứ phân vị của một mẫu số liệu gồm ba giá trị, gọi là tứ phân vị thứ nhất, thứ hai và thứ ba (lần lượt kí hiệu là Q$_{1}$, Q$_{2}$, Q$_{3}$). Ba giá trị này chia tập hợp dữ liệu đã sắp xếp thành bốn phần đều nhau. Cụ thể:

• Giá trị tứ phân vị thứ hai, Q$_{2}$, chính là số trung vị của mẫu.

• Giá trị tứ phân vị thứ nhất, Q$_{1}$, là trung vị của nửa số liệu đã sắp xếp bên trái Q$_{2}$ (không bao gồm Q$_{2}$ nếu n lẻ).

• Giá trị tứ phân vị thứ ba, Q$_{3}$, là trung vị của nửa số liệu đã sắp xếp bên phải Q$_{2}$ (không bao gồm Q nếu n lẻ).

Ý nghĩa của tứ phân vị:

Các điểm tứ phân vị Q$_{1}$, Q$_{2}$, Q$_{3}$ chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần chứa khoảng 25% tổng số  liệu đã thu thập được.

Tứ phân vị thứ nhất Q$_{1}$ còn được gọi là tứ phân vị dưới và đại diện cho nửa mẫu số liệu phía dưới. Tứ phân vị thứ ba Q$_{3}$ còn được gọi là tứ phân vị trên và đại diện cho nửa mẫu số liệu phía trên.

Ví dụ 4: SGK-tr116

Thực hành 2.

a) Sắp xếp lại mẫu số liệu theo thứ tự không giảm, ta được: 2; 2; 5; 7; 10; 10; 13; 15; 19.

Vì cỡ mẫu là n = 9, là số lẻ, nên giá trị tứ vị phân thứ hai là Q$_{2}$ = 10.

Tứ phân vị thứ nhất là trung vị của mẫu: 2; 2; 5; 7. Do đó Q$_{1}$ =$\frac{1}{2}$(2 + 5) = 3,5.

Tứ phân vị thứ ba là trung vị của mẫu: 10; 13; 15; 19. Do đó Q$_{3}$=$\frac{1}{2}$(13 + 15) = 14

b) Sắp xếp lại mẫu số liệu theo thứ tự không giảm, ta được: 1; 2; 5; 5; 9; 10; 10; 15; 15; 19.

Vì cỡ mẫu là n = 10, là số chẵn, nên giá trị tứ vị phân thứ hai là Q$_{2}$=$\frac{1}{2}$(9 + 10) = 9,5.

Tứ phân vị thứ nhất là trung vị của mẫu: 1; 2; 5; 5; 9. Do đó Q$_{1}$= 5.

Tứ phân vị thứ ba là trung vị của mẫu: 10; 10; 15; 15; 19. Do đó Q$_{3}$= 15.

3. MỐT

HĐKP4.

Từ bảng ta thấy, số lượng hoa hồng nhung bán được nhiều nhất (230 bông). Do đó, cửa hàng nền nhập hoa hồng nhung để bán trong ngày 14 tháng 2 năm tiếp theo.

⇒ Kết luận:

Cho một mẫu số liệu dưới bảng tần số. Giá trị có tần số lớn nhất được gọi là mốt của mẫu số liệu và kí hiệu là M$_{0}$.

Ví dụ 5: SGK-tr117

Ý nghĩa của mốt: Mốt đặc trưng cho giá trị xuất hiện nhiều nhất trong mẫu.

Chú ý: Một mẫu số liệu có thể có nhiều mốt. Khi tất cả các giá trị trong mẫu số liệu có tần số xuất hiện bằng nhau thì mẫu số liệu đó không có mốt.

Thực hành 3. 

Mẫu số liệu điểm kiểm tra của các bạn Tổ 1 có M$_{0}$= 6; 10.