Giải VNEN toán 9 bài 2: Đồ thị của hàm số y = ax^2 (a khác 0)
Giải bài 2: Đồ thị của hàm số y = ax^2 (a khác 0) - Sách hướng dẫn học toán 9 tập 2 trang 28. Sách này nằm trong bộ VNEN của chương trình mới. Dưới đây sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu, Hi vọng các em học sinh nắm tốt kiến thức bài học.
A. Hoạt động khởi động
Quan sát và liên tưởng (sgk trang 28)
B. Hoạt động hình thành kiến thức
1. Thực hiện các hoạt động sau
a) Điền vào ô trống giá trị của y tương ứng với mỗi giá trị của x trong bảng sau:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| $y = 2x^2$ |
b) Từ bảng trên, hãy viết vào chỗ chấm (...) để được tọa độ một số điểm thuộc đồ thị hàm số $y = 2x^2$ rồi xác định các điểm đó trên hệ trục tọa độ Oxy hình 6a (theo mẫu).

A(-3; 18); A'(3; ...); B(-2; ...); B'(2; ...); C(-1; ...); C'(1; ...); O(0; ...)
c) Đồ thị của hảm số $y = 2x^2$ là đường cong đi qua các điểm A, A', B, B', C, C', O như hình 6b.
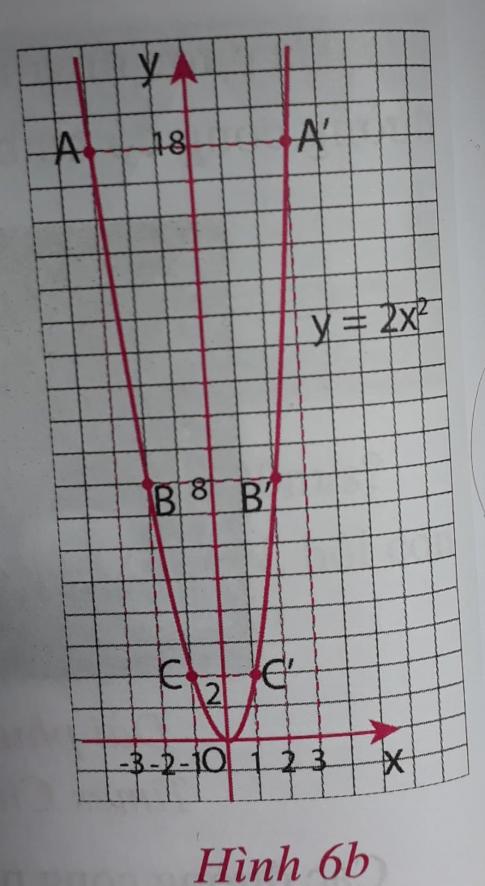
Hãy tô lại bằng bút chì đồ thị hàm số $y = 2x^2$ trong hình 6b rồi vẽ lại vào hình 6a.
d) Hãy nhận xét một vài đặc điểm của đồ thị hàm hàm số $y = 2x^2$ bằng cách trả lời câu hỏi sau:
Đồ thị nằm ở phía trên hay phía dưới trục hoành?
Vị trí của điểm A, A' đối với trục Oy ? Tương tự với các cặp điểm B, B' và C, C'?
Điểm nào là điểm thấp nhất của đồ thị?
Trả lời:
a)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| $y = 2x^2$ | 18 | 8 | 2 | 0 | 2 | 8 | 18 |
b) A(-3; 18); A'(3; 18); B(-2; 8); B'(2; 8); C(-1; 2); C'(1; 2); O(0; 0)
c) Các em vẽ lại hình 7b vào vở
d)
- Đồ thị nằm ở phía trên trục hoành
- Các cặp điểm A và A'; B và B'; C và C' đối xứng nhau qua trục tung.
- Điểm thấp nhất của đồ thị là điểm O
2. Thực hiện các hoạt động sau
a) Điền vào ô trống giá trị của y tương ứng với mỗi giá trị của x trong bảng sau:
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| $y = -\frac{1}{2}x^2$ |
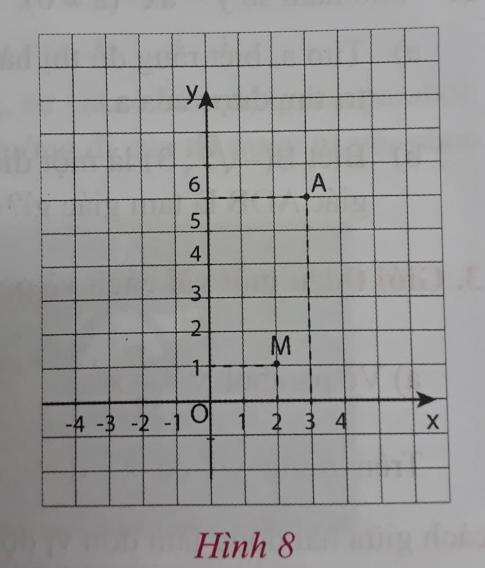
b) Từ bảng trên hãy viết tiếp vào chỗ chấm (...) để được tọa độ một số điểm thuộc đồ thị hàm số $y = -\frac{1}{2}x^2$ rồi xác định các điểm đó trên hệ trục tọa độ Oxy hình 7a (theo mẫu).
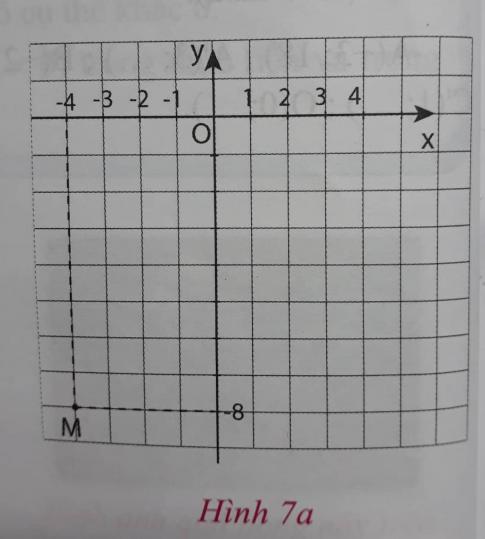
M(-4; -8); M'(4; ...); N(-2; ...); N'(2; ...); P(-1; ...); P'(1; ...); O(0; ...)
c) Đồ thị của hảm số $y = -\frac{1}{2}x^2$ là đường cong đi qua các điểm M, M', N, N', P, P', O như hình 7b.
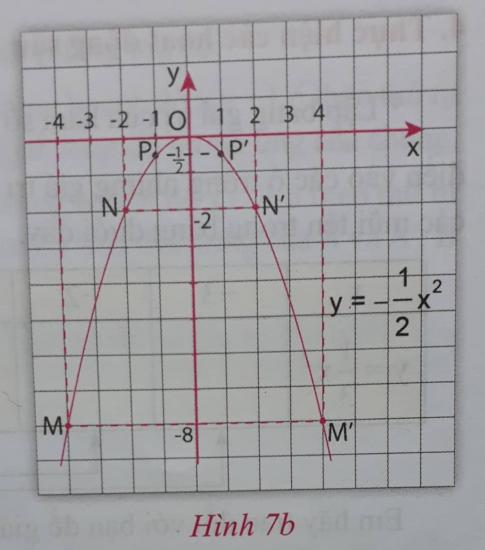
Hãy tô lại bằng bút chì đồ thị hàm số $y = -\frac{1}{2}x^2$ trong hình 7b rồi vẽ lại vào hình 7a.
d) Hãy nhận xét một vài đặc điểm của đồ thị hàm hàm số $y = -\frac{1}{2}x^2$ bằng cách trả lời câu hỏi sau:
Đồ thị nằm ở phía trên hay phía dưới trục hoành?
Vị trí của điểm M, M' đối với trục Oy ? Tương tự với các cặp điểm N, N' và P, P'?
Trả lời:
a)
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| $y = -\frac{1}{2}x^2$ | -8 | $\frac{-9}{2}$ | -2 | $\frac{-1}{2}$ | 0 | $\frac{-1}{2}$ | -2 | $\frac{-9}{2}$ | -8 |
b) M(-4; -8); M'(4; 8); N(-2; -2); N'(2; -2); P(-1; $\frac{-1}{2}$); P'(1; $\frac{-1}{2}$); O(0; 0)
c) Các em vẽ lại hình 7b vào vở
d)
- Đồ thị nằm phía dưới trục hoành
- Các cặp điểm đó đối xứng nhau qua trục Oy
- Điểm cao nhất của đồ thị là O(0; 0)
3. Đọc kĩ nội dung sau (sgk trang 31)
4. Thực hiện các hoạt động sau
Lập bảng giá trị của hàm số $y = \frac{1}{3}x^2$ ứng với x = 0; x = 1; x = 2; x = 3 vào vở rồi điền vào các ô trống những giá trị tương ứng với x = -1; x = -2; x = -3
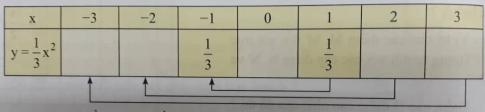
Em hãy trao đổi với bạn để giải thích tại sao làm được như vậy
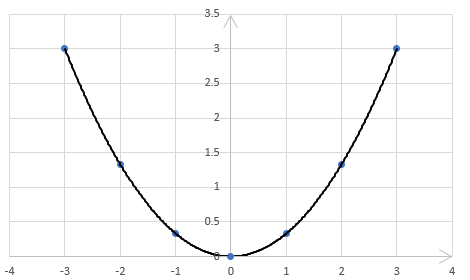
Vẽ đồ thị hàm số $y = \frac{1}{3}x^2$ vào vở
Trả lời:
| x | 0 | 1 | 2 | 3 |
| $y = \frac{1}{3}x^2$ | 0 | $\frac{1}{3}$ | $\frac{4}{3}$ | 3 |
Dựa vào tính đối xứng của hàm số qua trục Oy, ta có bảng sau:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| $y = \frac{1}{3}x^2$ | 3 | $\frac{4}{3}$ | $\frac{1}{3}$ | 0 | $\frac{1}{3}$ | $\frac{4}{3}$ | 3 |
Đồ thị hàm số:
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9


Bình luận