A. Hoạt động khởi động

sgk trang 85

B. Hoạt động hình thành kiến thức

1. Thực hiện các hoạt động sau để hiểu về góc nội tiếp

a) Đọc, làm theo và trả lời các câu hỏi

Chuẩn bị một hình tròn tâm O bán kính R bằng giấy mỏng. Dùng kéo cắt theo hai dây cung BA, BC.

Góc ABC có gì đặc biệt về đỉnh?

Số đo của $\widehat{ABC}$ có liên hệ gì với số đo cung nhỏ AC?

b) Đọc kĩ nội dung sau (sgk trang 86)

c) Luyện tập, ghi vào vở

Vẽ đường tròn (O; R). Vẽ một góc nội tiếp đường tròn (O). Vẽ một góc không phải là góc nội tiếp đường tròn (O).

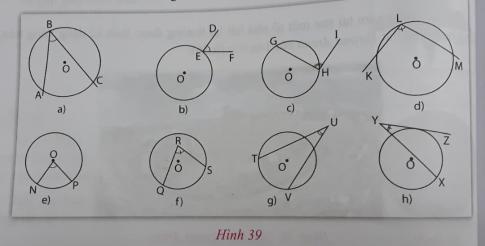
Xem hình 39 và cho biết góc nào không phải góc nội tiếp? Vì sao?

Trả lời:

a) $\widehat{ABC} = \frac{1}{2}$ sđ AC

c) 

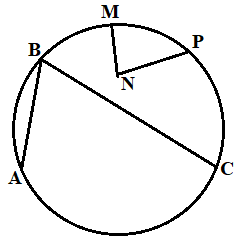
Trong hình trên góc ABC là góc nội tiếp, góc MNP không phải góc nội tiếp.

Trong hình 39: Chỉ có hình a là góc nội tiếp.

2. Thực hiện các hoạt động sau để hiểu liên hệ giữa số đo góc nội tiếp và số đo cung bị chắn

a) Đọc, làm theo và trả lời các câu hỏi

Xem hình 40 và cho biết:

• Số đo cung nhỏ AC bằng bao nhiêu?
• Cho biết số đo góc CDA bằng bao nhiêu?
• Có nhận xét gì về mối liên hệ giữa số đo góc nội tiếp CDA và số đo cung bị chắn AC?

Xem hình 41

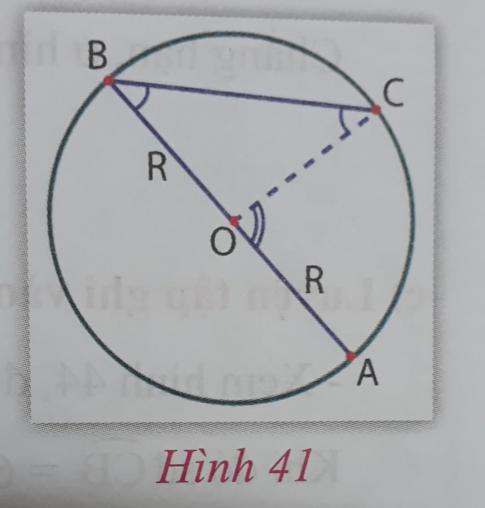
• BOC có phải là tam giác cân hay không? Vì sao?
• Chứng tỏ rằng $\widehat{AOC} = \widehat{ABC} + \widehat{BCO}$
• Từ đó suy ra $\widehat{AOC} = 2\widehat{ABC}$.
• Có hay không: $\widehat{ABC} = \frac{1}{2}sđ AC$ (*)

Xem hình 42: Đường kính BD chia $\widehat{ABC}$ thành hai góc là $\widehat{ABD}$ và $\widehat{CBD}$

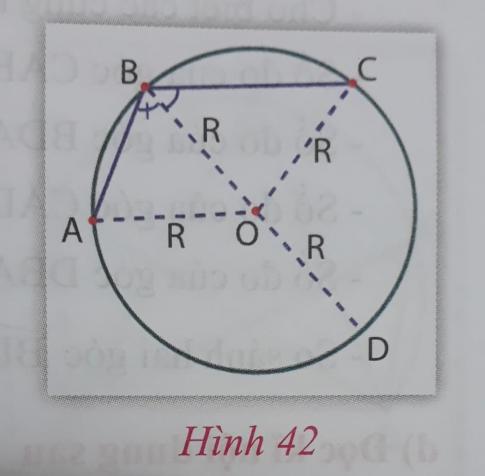
• BOA có phải là tam giác cân hay không? Vì sao?
• Chứng tỏ rằng $\widehat{AOD} = \widehat{ABO} + \widehat{BAO}$
• Từ đó suy ra $\widehat{AOD} = 2\widehat{ABO}$
• Có hay không: $\widehat{ABO} = \frac{1}{2}sđ CD$?
• Tương tự, chứng tỏ rằng $\widehat{COD} = \widehat{CBO} + \widehat{BCO}$
• Từ đó suy ra $\widehat{COD} = 2\widehat{CBO}$
• Có hay không $\widehat{OBC} = \frac{1}{2} sđ CD$?
• Khi đó, có hay không: $\widehat{ABC} = \frac{1}{2} sđ AC$ (**)

Xem hình 43.

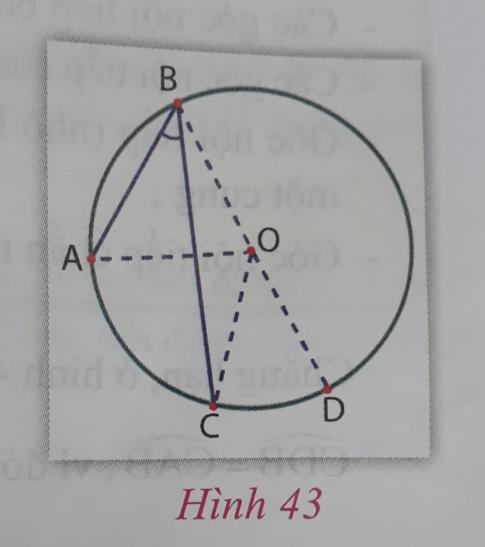
• Chứng tỏ $\widehat{ABO} = \frac{1}{2} \widehat{AOD}$ và $\widehat{CBO} = \frac{1}{2}\widehat{COD}$
• Từ đó, suy ra: $\widehat{ABC} = \widehat{ABO} - \widehat{CBO} = \frac{1}{2}(\widehat{AOD} - \widehat{COD}) = \frac{1}{2} \widehat{AOC}$.
• Có hay không: $\widehat{ABC} = \frac{1}{2} sđ AC$

Từ (*), (**), (***) có thể suy ra: Số đo của góc nội tiếp bằng nửa số đo của cung bị chắn?

b) Đọc kĩ nội dung sau (sgk trang 88)

c) Luyện tập, ghi vào vở

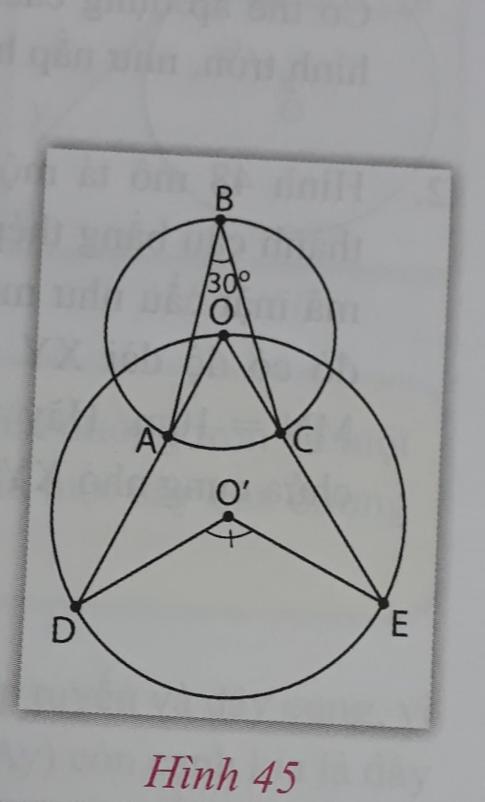
Xem hình 44, dường tròn (O) có CD = CB = BA = CO = OB = OA = OD = R.

Khi đó sđ CB = $60^\circ$

Góc nội tiếp $\widehat{CDB}$ chắn cung nhỏ CB, nên $\widehat{CDB} = 30^\circ$.

• Cho biết các cung nhỏ bằng nhau trên hình đó.
• Số đo của góc CAB bằng bao nhiêu? Vì sao?
• Số đo của góc BDA bằng bao nhiêu? Vì sao?
• Số đo của góc CAD bằng bao nhiêu? Vì sao?
• Số đo của góc DBA bằng bao nhiêu? Vì sao?
• So sánh hai góc $\widehat{BDA}$ và $widehat{CAD}$?

d) Đọc kĩ nội dung sau (sgk trang 88)

Trả lời:

a) 

Hình 40:

• Sđ AC = $120^\circ$
• $\widehat{CDA} = 60^\circ$ 
• $\Rightarrow \widehat{CDA} = \frac{1}{2} sđ AC$

Hình 41:

• BOC là tam giác cân tại O
• $\widehat{AOC} = \widehat{ABC} + \widehat{BCO}$ (Tính chất góc ngoài của tam giác)
• $\Rightarrow \widehat{AOC} = 2\widehat{ABC}$.
• $\Rightarrow \widehat{ABC} = \frac{1}{2}sđ AC$ (*)

Xem hình 42: Đường kính BD chia $\widehat{ABC}$ thành hai góc là $\widehat{ABD}$ và $\widehat{CBD}$

• BOA là tam giác cân tại O vì OA = OB = R
• $\widehat{AOD} = \widehat{ABO} + \widehat{BAO}$ (Tính chất góc ngoài của tam giác)
• $\Rightarrow \widehat{AOD} = 2\widehat{ABO}$
• $\widehat{ABO} = \frac{1}{2}sđ CD$
• Tương tự: $\widehat{COD} = widehat{CBO} + \widehat{BCO}$
• $\Rightarrow \widehat{COD} = 2\widehat{CBO}$
• $\Rightarrow \widehat{OBC} = \frac{1}{2} sđ CD$
• $\Rightarrow \widehat{ABC} = \frac{1}{2} sđ AC$ (Theo tính chất cộng của góc và cung)

Xem hình 43.

• Tương tự, ta có: $\widehat{ABO} = \frac{1}{2} \widehat{AOD}$ và $\widehat{CBO} = \frac{1}{2}\widehat{COD}$
• $\Rightarrow \widehat{ABC} = \widehat{ABO} - \widehat{CBO} = \frac{1}{2}(\widehat{AOD} - \widehat{COD}) = \frac{1}{2} \widehat{AOC}$.
• $\Rightarrow \widehat{ABC} = \frac{1}{2} sđ AC$

Từ (*), (**), (***) có thể suy ra: Số đo của góc nội tiếp bằng nửa số đo của cung bị chắn

c)

• Các cung nhỏ bằng nhau trên hình 44 là: cung AB = cung BC = cung CD; cung AC = cung BD.
• $\widehat{CAB} = \frac{1}{2} sd CB = \frac{1}{2}\widehat{COB} = \frac{60^\circ}{2} = 30^\circ$
• $\widehat{BDA} = \frac{1}{2} sd AB = \frac{1}{2}\widehat{AOB} = \frac{60^\circ}{2} = 30^\circ$
• $\widehat{CAD} = \frac{1}{2} sd CD = \frac{1}{2}\widehat{COD} = \frac{60^\circ}{2} = 30^\circ$
• $\widehat{DBA} = \frac{1}{2} sd AD = \frac{1}{2}\widehat{AOD} = \frac{60^\circ}{2} = 30^\circ$
• $\widehat{BDA} = \widehat{CAD} = 30^\circ$?