Đề thi cuối kì 1 Toán 9 CTST: Đề tham khảo số 3
Trọn bộ Đề thi cuối kì 1 Toán 9 CTST: Đề tham khảo số 3 bộ sách mới Chân trời sáng tạo gồm nhiều câu hỏi ôn tập hay, các dạng bài tập phong phú giúp các em củng cố ôn luyện lại kiến thức thật tốt chuẩn bị tốt cho kì thi sắp tới. Tài liệu có kèm theo đáp án và lời giải chi tiết. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt điểm cao. Thầy cô và các em kéo xuống để tham khảo ôn luyện
ĐỀ KIỂM TRA HỌC KÌ 1
TOÁN 9 – CHÂN TRỜI SÁNG TẠO
A. PHẦN TRẮC NGHIỆM (4 điểm)
Khoanh tròn vào chữ cái đứng trước câu trả lời đúng:
Câu 1. Điều kiện xác định của phương trình ![]() là:
là:
A. ![]() và
và ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 2. Khẳng định nào sau đây là sai?
A. ![]() nếu
nếu ![]()
B. ![]() khi
khi ![]()
C. ![]() khi
khi ![]()
D. ![]() nếu
nếu ![]()
Câu 3. Khẳng định nào sau đây là đúng?
A. Nếu ![]() thì
thì ![]()
B. Nếu ![]() thì
thì ![]()
C. Nếu ![]() thì
thì ![]()
D. Nếu ![]() thì
thì ![]()
Câu 4. ![]() bằng:
bằng:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 5. Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng?
A. AB > CD
B. AB < CD
C. AB = CD
D. AB ![]() CD
CD
Câu 6. Bất phương trình ![]() có tập nghiệm là:
có tập nghiệm là:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 7. Nghiệm của hệ phương trình 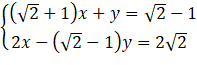
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 8. Tính giá trị của biểu thức ![]() khi
khi ![]() ?
?
A. 29
B. 25
C. 10
D. 5
Câu 9. Cho hai đường tròn (O; R) và (O’; r) với R > r cắt nhau tại hai điểm phân biệt và OO’ = d. Chọn khẳng định đúng.
A. R – r < d < R + r
B. d = R – r
C. d > R + r
D. d < R + r
Câu 10. Số đo no của cung tròn có độ dài 30,8cm trên đường tròn có bán kính 22cm là (lấy π ≈ 3,14 và làm tròn đến độ)
A. 70o
B. 80o
C. 65o
D. 85o
PHẦN TỰ LUẬN (6 điểm)
Bài 1. (1 điểm). Tính giá trị biểu thức
a) ![]()
b) ![]() -
- ![]() -
- ![]()
Bài 2. (2 điểm). Cho hai biểu thức ![]() và
và ![]() với
với ![]()
a) Tính giá trị của biểu thức ![]() khi
khi ![]()
b) Rút gọn biểu thức ![]()
c) Tìm các giá trị nguyên của ![]() để biểu thức
để biểu thức ![]() có giá trị nguyên
có giá trị nguyên
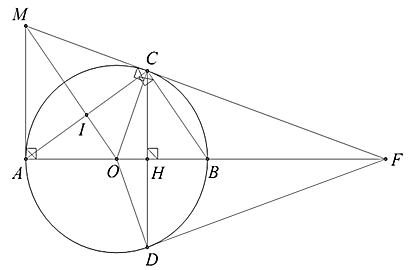
Bài 3. (2,5 điểm). Cho đường tròn (O; R), đường kính AB. Lấy điểm C thuộc (O; R) sao cho AC > BC. Kẻ đường cao CH của ![]() ABC (H
ABC (H![]() AB), kéo dài CH cắt (O; R) tại điểm D (D ≠ C). Tiếp tuyến tại điểm A và tiếp tuyến tại điểm C của đường tròn (O; R) cắt nhau tại điểm M. Gọi I là giao điểm của OM và AC. Hai đường thẳng MC và AB cắt nhau tại F.
AB), kéo dài CH cắt (O; R) tại điểm D (D ≠ C). Tiếp tuyến tại điểm A và tiếp tuyến tại điểm C của đường tròn (O; R) cắt nhau tại điểm M. Gọi I là giao điểm của OM và AC. Hai đường thẳng MC và AB cắt nhau tại F.
a) Chứng minh DF là tiếp tuyến của (O; R).
b) Chứng minh BC = 2.IO
c) Chứng minh: AF.BH = BF.AH
Bài 4. (0,5 điểm). Giải phương trình: ![]()
TRƯỜNG THCS ........
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KÌ 1 (2024 – 2025)
MÔN: TOÁN 9 – CHÂN TRỜI SÁNG TẠO
A. PHẦN TRẮC NGHIỆM: (4 điểm)
Mỗi câu trả lời đúng được 0,4 điểm.
Câu 1 | Câu 2 | Câu 3 | Câu 4 | Câu 5 | Câu 6 | Câu 7 | Câu 8 | Câu 9 | Câu 10 |
A | B | C | D | A | B | C | D | A | B |
B. PHẦN TỰ LUẬN: (6 điểm)
Câu | Nội dung đáp án |
Bài 1 (1 điểm) | a)
|
b) = = | |
Bài 2 (2 điểm) | a) Thay
Vậy |
b) Với
Vậy | |
c) Để Ta có: Mà Kết hợp điều kiện: Vậy không có giá trị của |
Bài 3 (2,5 điểm) |
|
a) Xét Mà OH là đường cao của Chứng minh được:
Mà Do Xét (O; R) có: OD Suy ra: DF là tiếp tuyến của (O; R) tại D (đpcm) | |
b) Xét (O; R) có: MA và MC là hai tiếp tuyến cắt nhau tại M.
Xét Mà OM là tia phân giác của Mà O là trung điểm của AB nên IO là đường trung bình của
|

Bài 4 (0,5 điểm) | Ta có: Điều kiện xác định: Đặt:
Phương trình:
Do đó:
hay Vậy phương trình đã cho có nghiệm duy nhất |
Đề thi Toán 9 Chân trời sáng tạo, trọn bộ đề thi Toán 9 Chân trời sáng tạo, Đề thi cuối kì 1 Toán 9 CTST:
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

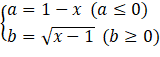
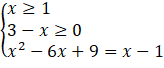
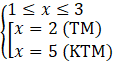
Bình luận