Video giảng Toán 8 kết nối bài 15 Định lí Thales trong tam giác

Tóm lược nội dung

CHƯƠNG 4. ĐỊNH LÍ THALES

BÀI 15: ĐỊNH LÍ THALES TRONG TAM GIÁC

Xin chào các em học sinh thân mến, chúng ta lại gặp nhau trong bài học ngày hôm nay rồi!

Thông qua video này, các em sẽ nắm được các kiến thức và kĩ năng như sau:

• Phát biều được khái niệm tỉ số của hai đoạn thẳng, đoạn thẳng tỉ lệ.
• Phát biểu được định lí Thalès thuận và định lí Thalès đảo.

HOẠT ĐỘNG KHỞI ĐỘNG

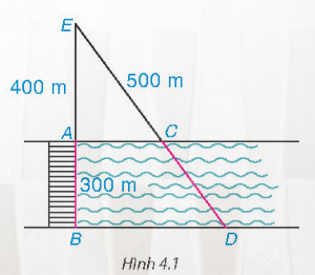
Trước khi bước vào bài học ngày hôm nay, các em đọc tình huống mở đầu: Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào.

HOẠT ĐỘNG KHÁM PHÁ

Nội dung 1: Đoạn thẳng tỉ lệ

Theo em, đoạn thẳng tỉ lệ là gì?

Video trình bày nội dung:

Tỉ số của hai đoạn thẳng

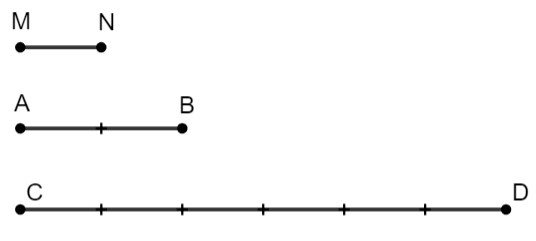
Hoạt động 1:

AB = 2 MN

CD = 6 MN

Hoạt động 2:

AB = 3 cm

CD = 9 cm

Hoạt động 3: 

Tỉ số tìm được trong hai đoạn thẳng trên bằng nhau.

Nhận xét:

Khi thay đổi đơn vị đo, tỉ số độ dài của hai đoạn thẳng AB và CD không thay đổi.

Kết luận:

Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Luyện tập 1:

a)

b) HK = 10 dm = 100 cm

Kết luận:

Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức:

hay

Nội dung 2: Định lý thales trong tam giác

Em hãy phát biểu định lý Thales?

Video trình bày nội dung:

2.1. Định lí Thalès

Kết luận:

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

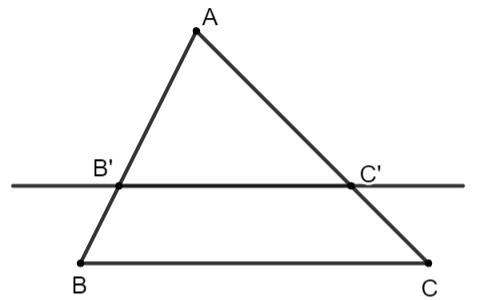
GT	ABC, B’C’ // BC (B’  AB; C’  AC)
KL

Ví dụ 1 (SGK – tr.78):

Xét tam giác DEF có MN // EF nên theo định lí Thalès, ta có: 

hay , suy ra

Luyện tập 3:

a) Xét tam giác ABC có MN // BC nên theo định lí Thalès, ta có:

hay , suy ra

b) Ta có EF  PH; HQ  PH nên EF // HQ

Xét tam giác HPQ có EF // HQ nên theo định lí Thalès, ta có:

hay , suy ra

2.2. Định lí Thalès trong tam giác

Định lí Thalès đảo

Hoạt động 4:

Xét tam giác ABC có B’C” // BC nên theo định lí Thalès, ta có:

hay , suy ra  cm

Có AC’ = 6 cm; AC” = 6cm

Suy ra AC’ = AC”

Vậy C’ trùng với C”

Vì  mà  => .

Kết luận:

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác

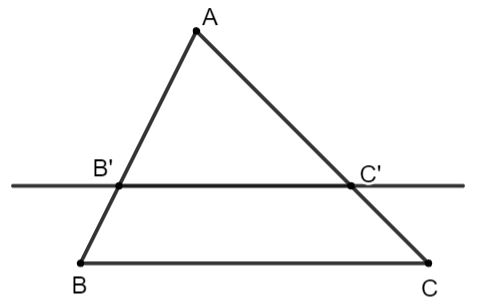
GT	ABC (B’  AB; C’  AC),
KL	B’C’ // BC

Ví dụ 2 (SGK – tr.79):

Xét tam giác DEF, ta có: ;

Vì  nên MN // EF (định lí Thalès đảo).

Vận dụng:

Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD

Xét tam giác ABC có AC // BD nên theo định lí Thalès, ta có:

hay

Suy ra  (m)

Vậy khoảng cách giữa C và D bằng 375 m.

………..

Nội dung video Bài 15: Định lí Thales trong tam giác còn nhiều phần rất hấp dẫn và thú vị. Hãy cùng đăng kí để tham gia học bài và củng cố kiến thức thông qua hoạt động luyện tập và vận dụng trong video.