Slide bài giảng toán 6 cánh diều bài 6: Phép Chia Hết Hai Số Nguyên. Quan Hệ Chia Hết Trong Tập Hợp Số Nguyên ( 3 Tiết)

Tóm lược nội dung

CHƯƠNG II: SỐ NGUYÊN

BÀI 6: PHÉP CHIA HẾT HAI SỐ NGUYÊN. QUAN HỆ CHIA HẾT TRONG TẬP HỢP SỐ NGUYÊN

1. PHÉP CHIA HAI SỐ NGUYÊN KHÁC DẤU

Bài 1: 

a) Tìm số thích hợp cho (?) : Do (– 3) . (– 4) = 12 nên 12 : (– 3) = (?)

Mẫu: Do 4 . (– 3) = – 12 nên (– 12) : 4 = – 3.

b) So sánh 12 : (– 3) và – (12 : 3).

Trả lời rút gọn:

a) Do (– 3) . (– 4) = 12 nên 12 : (– 3) = – 4. 

Vậy số thích hợp cần điền vào (?) là – 4.

b) Theo câu a) ta có: 12 : (– 3) = – 4

Ta có: – (12 : 3) = – 4 

Vậy 12 : (– 3) = – (12 : 3).

Bài 2: Tính:

a) 36 : (– 9);

b) (– 48) : 6.

Trả lời rút gọn:

a) 36 : (– 9) = – (36 : 9) = – 4.

b) (– 48) : 6 = – (48 : 6) = – 8. 

2. PHÉP CHIA HẾT HAI SỐ NGUYÊN CÙNG DẤU

Bài 1: 

a) Tìm số thích hợp cho (?) : Do (– 5) . 4 = – 20 nên (– 20) : (– 5) = (?)

Mẫu: Do (– 4) . 3 = – 12 nên (– 12) : (– 4) = 3.

b) So sánh (– 20) : (– 5) và 20 : 5.

Trả lời rút gọn: 

a) Do (– 5) . 4 = – 20 nên (– 20) : (– 5) = 4

Vậy số thích hợp cần điền vào dấu (?) là 4. 

b) Theo câu a ta có: (– 20) : (– 5) = 4

Lại có: 20 : 5 = 4

Vậy (– 20) : (– 5) = 20 : 5. 

Bài 2: Tính:

a) (– 12) : (– 6);

b) (– 64) : (– 8).

Trả lời rút gọn: 

a) (– 12) : (– 6) = 12 : 6 = 2. 

b) (– 64) : (– 8) = 64 : 8 = 8.

3. QUAN HỆ CHIA HẾT

Bài 1: a) Tìm số thích hợp ở (?) trong bảng sau:

b) Số – 36 có thể chia hết cho các số nguyên nào?

Trả lời rút gọn: 

a) Ta có: (– 36) : 3 = – (36 : 3) = – 12

(– 36) : 4 = – (36 : 4) = – 9

(– 36) : 6 = – (36 : 6) = – 6

(– 36) : 9 = – (36 : 9) = – 4

(– 36) : 12 = – (36 : 12) = – 3

(– 36) : 18 = – (36 : 18) = – 2

(– 36) : 36 = – (36 : 36) = – 1

Khi đó, ta điền được các số vào bảng như sau: 

b) Theo câu a ta thấy số – 36 có thể chia hết cho các số nguyên là 1; 2; 3; 4; 6; 9; 12; 18; 36; – 1; – 2; – 3; – 4; – 6; – 9; – 12; – 18; – 36. 

Bài 2: Sử dụng các từ “chia hết cho”, "bội", “ước” thích hợp (?):

a) – 16 (?) – 2;

b) – 18 là (?) của – 6;

c) 3 là (?) của – 27.

Trả lời rút gọn: 

a) Vì – 16 = (– 2) . 8 

Nên số – 16 chia hết cho số – 2

Vậy từ thích hợp điền vào dấu (?) là "chia hết cho".

b) Vì – 18 = (– 6) . 3 

Nên – 18 là bội của – 6

Vậy từ thích hợp điền vào dấu (?) là "bội".

c) Vì – 27 = 3 . (– 9) 

Nên 3 là ước của – 27

Vậy từ thích hợp điền vào dấu (?) là "ước". 

Bài 3: 

a) Viết tất cả các số nguyên là ước của: – 15; – 12.

b) Viết năm số nguyên là bội của: – 3; – 7. 

Trả lời rút gọn: 

a) 

+) Ta có: – 15 = (– 1) . 15 = 1 . (– 15)  = 3 . (– 5) = (– 3) . 5 

Do đó các ước của – 15 là: – 1; 1; – 3; 3; –5; 5; –15; 15.

+) Lại có: – 12 = (– 1) . 12 = 1 . (– 12) = 2 . (– 6) = (– 2) . 6 = 3 . (– 4) = (– 3) . 4

Do đó các ước của – 12 là: – 1; 1; – 2; 2; – 3; 3; – 4; 4; – 6; 6; – 12; 12.

b) 

+) Ta có: (– 3) . 1 = – 3; (– 3) . (– 1) = 3; (– 3) . 2 = – 6; (– 3) . (– 2) = 6; (– 3) . 3 = – 9

Do đó năm số nguyên là bội của – 3 là: – 3; 3; – 6; 6; – 9.

+) Ta có: (– 7) . 0 = 0; (– 7) . 1 = – 7; (– 7) . (– 1) = 7; (– 7) . 2 = – 14; (– 7) . (– 2) = 14

Do đó năm số nguyên là bội của – 7 là: 0; – 7; 7; – 14; 14.

BÀI TẬP

Bài 1: Tính:

a) (– 45) : 5; 

b) 56 : (– 7); 

c) 75 : 25; 

d) (– 207) : (– 9).

Trả lời rút gọn: 

a) (– 45) : 5 = – (45 : 5) = – 9. 

b) 56 : (– 7) = – (56 : 7) = – 8.

c) 75 : 25 = 3.

d) (– 207) : (– 9) = 207 : 9 = 23.

Bài 2: So sánh:

a) 36 : (– 6) và 0; 

b) (– 15) : (– 3) và (– 63) : 7.

Trả lời rút gọn: 

a) Ta có: 36 : (– 6) = – (36 : 6) = – 6 < 0 

Vậy 36 : (– 6) < 0.

b) Ta có: (– 15) : (– 3) = 15 : 3 = 5 > 0

(– 63) : 7 = – (63 : 7) = – 9 < 0

Do đó: 5 > – 9

Vậy (– 15) : (– 3) > (– 63) : 7. 

Bài 3: Tìm số nguyên x, biết:

a) (– 3) . x = 36; 

b) (– 100) : (x + 5) = – 5.

Trả lời rút gọn: 

a) (– 3) . x = 36 

               x = 36 : (– 3) 

            x = – (36 : 3) 

               x = – 12. 

Vậy x = – 12. 

b) (– 100) : (x + 5) = – 5

                     x + 5 = (– 100) : (– 5) 

                     x + 5 = 100 : 5

                     x + 5 = 20 

                     x       = 20 – 5 

                     x       = 15. 

Vậy x = 15. 

Bài 4: Nhiệt độ lúc 8 giờ sáng trong 5 ngày liên tiếp là – 6 °C, – 5 °C, – 4 °C, 2 °C, 3 °C. Tính nhiệt độ trung bình lúc 8 giờ sáng của 5 ngày đó.

Trả lời rút gọn: 

Nhiệt độ trung bình lúc 8 giờ sáng của 5 ngày liên tiếp đã cho là – 2 °C. 

Bài 5: Trong các phát biểu sau đây, phát biểu nào đúng, phát biểu nào sai? Giải thích.

a) – 36 chia hết cho – 9, 

b) – 18 chia hết cho 5.

Trả lời rút gọn: 

a) Ta có: – 36 = (– 9) . 4 hay (– 36) : (– 9) = 4 

Do đó: – 36 chia hết cho – 9. 

Vậy phát biểu a) đúng. 

b) Ta có: – 18 = 5 . (– 3) + (– 3) 

Do đó – 18 không chia hết cho 5. 

Vậy phát biểu b) là sai. 

Bài 6: Tìm số nguyên x, biết:

a) 4 chia hết cho x; 

b) – 13 chia hết cho x + 2.

Trả lời rút gọn: 

a) Vì 4 chia hết cho x nên x là các ước của 4 

Mà các ước của 4 là: – 1; 1; – 2; 2; – 4; 4 

Vậy các số nguyên x thỏa mãn yêu cầu là: – 1; 1; – 2; 2; – 4; 4.

b) Vì – 13 chia hết cho x + 2 nên x + 2 là ước của – 13

Mà các ước của – 13 là: – 1; 1; 13; – 13

Nên ta có các trường hợp sau:

TH1: x + 2 = – 1  x = – 1 – 2 = – 3 (tm)

TH2: x + 2 = 1  x = 1 – 2 = – 1 (tm)

TH3: x + 2 = 13  x = 13 – 2 = 11 (tm)

TH4: x + 2 = – 13  x = – 13 – 2 = – 15 (tm)

Vậy các số nguyên x thỏa mãn yêu cầu bài toán là: – 3; – 1; 11; – 15.

Bài 7: Một con ốc sên leo lên một cây cao 8 m. Trong mỗi ngày (24 giờ), 12 giờ đầu tiên ốc sên leo lên được 3 m, rồi 12 giờ sau nó lại tụt xuống 2 m. Quy ước quãng đường mà ốc sên leo lên 3 m là 3 m, quãng đường ốc sên tụt xuống 2 m là – 2 m.

a) Viết phép tính biểu thị quãng đường mà ốc sên leo được sau 2 ngày.

b) Sau 5 ngày thi ốc sên leo được bao nhiêu mét?

c) Sau bao nhiêu giờ thi ốc sên chạm đến ngọn cây? Biết rằng lúc 0 giờ ốc sên ở gốc cây và bắt đầu leo lên.

Trả lời rút gọn: 

a) [3 + (– 2)] . 2         (m)

b) Sau 5 ngày, ốc sên leo được số m là: 

[3 + (– 2)] . 5 = 5 (m) 

c) Sau 172 giờ leo cây thì ốc sên chạm đến ngọn cây. 

Bài 8: Sử dụng máy tính cầm tay

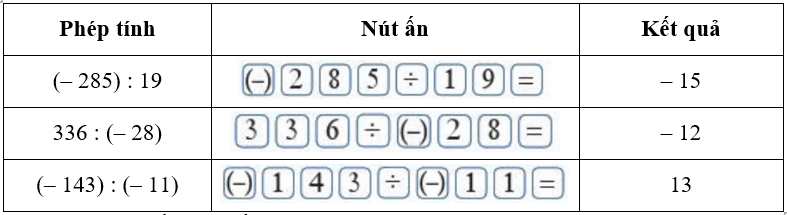
Dùng máy tính cầm tay để tính:

(– 252) : 21; 

253 : (– 11);

 (– 645) : (– 15).

Trả lời rút gọn: 

(– 252) : 21 = – 12;

253 : (– 11) = – 23;

(– 645) : (– 15) = 43.