Slide bài giảng toán 6 cánh diều bài 13: Bội Chung Và Bội Chung Nhỏ Nhất (3 Tiết)

Tóm lược nội dung

CHƯƠNG 1: SỐ TỰ NHIÊN

BÀI 13: BỘI CHUNG VÀ BỘI CHUNG NHỎ NHẤT

1. BỘI CHUNG VÀ BỘI CHUNG NHỎ NHẤT

Bài 1: a) Nêu một số bội của 2 và của 3 theo thứ tự tăng dần:

b) Tìm các số vừa ở trong hàng thứ nhất vừa ở trong hàng thứ hai. 

c) Xác định số nhỏ nhất khác 0 trong các bội chung của 2 và 3.

Trả lời rút gọn:

a)

b) Các số vừa ở hàng thứ nhất vừa ở hàng thứ 2 là: 0, 6, 12, 18.

c) Số nhỏ nhất khác 0 trong bội chung của 2 và 3 là: 6.

Bài 2: Hãy nêu bốn bội chung của 5 và 9.

Trả lời rút gọn:

+ Trước tiên ta tìm các bội của 5 và 9.

+ Để tìm bội của 5, ta lần lượt lấy 5 nhân với các số 0; 1; 2; 3;…

+ Để tìm bội của 9, ta lần lượt lấy 9 nhân với các số 0; 1; 2; 3;…

Một số bội của 9 là: 0; 18; 27; 36; 45; 54; 63; 72; 81; 90; 99; 108; 117; 126; 135.

Do đó 4 bội chung của 5 và 9 là: 0; 45; 90; 135. 

Bài 3: Quan sát bảng sau:

a) Viết ba bội chung của 8 và 12 theo thứ tự tăng dần.

b) Tìm BCNN(8, 12).

c) Thực hiện phép chia ba bội chung của 8 và 12 cho BCNN(8, 12).

Trả lời rút gọn:

a) Quan sát bảng ta thấy các bội chung của 8 và 12 là: 0; 24; 48; 72.

b)  Trong các bội chung của 8 và 12 ở trên, ta thấy số 24 là số bé nhất và khác 0 nên BCNN(8, 12) = 24. 

c) Chia 3 bội chung của 8 và 12 cho BCNN(8, 12)

24 : 24 = 1

48 : 24 = 2

72 : 24 = 3. 

Bài 4: Tìm tất cả các số có ba chữ số là bội chung của a và b, biết rằng BCNN(a, b) = 300.

Trả lời rút gọn:

Tất cả các số có ba chữ số là bội chung của a và b là: 300; 600; 900.

1. TÌM BỘI CHUNG NHỎ NHẤT BẰNG CÁCH PHÂN TÍCH CÁC SỐ RA THỪA SỐ NGUYÊN TỐ

Bài 1: Ta có thể tìm BCNN(6,8) ...

Trả lời rút gọn:

Ta có thể tìm BCNN(6, 8) theo các bước sau:

Bước 1. Phân tích 6 và 8 ra thừa số nguyên tố

          6 = 2 . 3

          8 = 2 . 2 . 2 = 2³

Bước 2. Chọn ra các thừa số nguyên tố chung và các thừa số nguyên tố riêng của 6 và 8 lần lượt là 2 và 3.

Bước 3. Với mỗi thừa số nguyên tố 2 và 3, ta chọn lũy thừa với số mũ lớn nhất

+) Số mũ lớn nhất của 2 là 3; ta chọn 2³.

+) Số mũ lớn nhất của 3 là 1; ta chọn 3¹.

Bước 4. Lấy tích của các lũy thừa đã chọn, ta nhận được bội chung nhỏ nhất cần tìm BCNN(6, 8) = 2³ . 3¹ = 24.

Bài 2: Tìm bội chung nhỏ nhất của 12, 18, 27.

Trả lời rút gọn:

+ Ta phân tích các số 12, 18, 27 ra thừa số nguyên tố:

12 = 4 . 3 = 2² . 3 

18 = 2 . 9 = 2 . 3² 

27 = 3³ 

+ Các thừa số nguyên tố chung và riêng của 12, 18 và 27 là 2 và 3.

Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 3 

Vậy BCNN(12, 18, 27) = 2² . 3³ = 4 . 27 = 108.

1. ỨNG DỤNG BỘI CHUNG NHỎ NHẤT VÀO CỘNG, TRỪ CÁC PHÂN SỐ KHÔNG CÙNG MẪU

Bài 1: Thực hiện phép tính...

Trả lời rút gọn:

+) Ở tiểu học, ta đã làm như sau:

Quy đồng mẫu hai phân số bằng cách chọn mẫu chung là tích của hai mẫu:

Mẫu chung = 12 . 18 = 216

Ta có: 

.

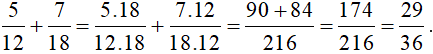Vậy

 .

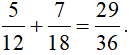+) Để tính tổng hai phân số trên, ta có thể làm như sau:

- Chọn mẫu chung là BCNN của các mẫu. Cụ thể: 

Mẫu chung = BCNN(12, 18) = 36

- Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu), ta có:

36 : 12 = 3; 36 : 18 = 2

- Sau khi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng, ta cộng hai phân số có cùng mẫu:

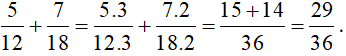
Bài 2: Thực hiện phép tính...

Trả lời rút gọn: 

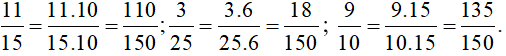
Vậy 

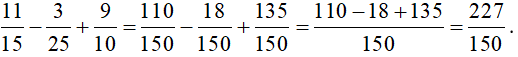
BÀI TẬP

Bài 1: 

a) Hãy viết các ước của 7 và các ước của 8. Tìm ƯCLN(7, 8).

b) Hai số 7 và 8 có nguyên tố cùng nhau hay không? Vì sao?

c) Tìm BCNN(7, 8). So sánh bội chung nhỏ nhất với tích hai số 7 và 8.

Trả lời rút gọn: 

a) ƯCLN(7, 8) = 1.

b) Vì ƯCLN(7, 8) = 1 (theo câu a) nên hai số 7 và 8 là hai số nguyên tố cùng nhau. 

c) Ta nói bội chung nhỏ nhất của hai số nguyên tố cùng nhau 7 và 8 chính bằng tích của hai số 7 và 8. 

Bài 2: Quan sát hai thanh sau:

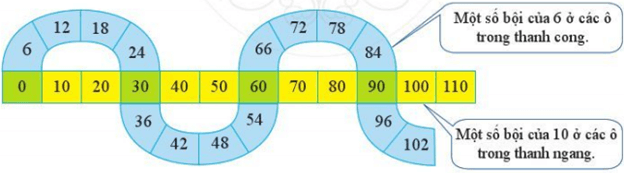
a) Số 0 có phải là bội chung của 6 và 10 không? Vì sao?

b) Viết bốn bội chung của 6 và 10 theo thứ tự tăng dần.

c) Tìm BCNN(6, 10).

d) Tìm các bội chung của 6 và 10 mà nhỏ hơn 160.

Trả lời rút gọn: 

a) Quan sát hình trên, ta thấy số 0 nằm trên cả 2 thanh, thanh một số bội của 10 (thanh ngang) và thanh một số bội của 6 (thanh cong) nên số 0 là bội chung của 6 và 10. 

Mở rộng: Hơn nữa, 0 chia hết cho tất cả các số tự nhiên khác 0 nên 0 là bội của mọi số tự nhiên khác 0. 

b) Quan sát hình trên, ta thấy các số 0; 30; 60; 90 (được tô màu đậm hơn) nằm trên cả hai thanh ngang và thanh cong.

Do đó bốn bội chung của 6 và 10 được xếp theo thứ tự tăng dần là: 0; 30; 60; 90.

 c) Trong các bội chung trên của 6 và 10, ta thấy 30 là số bé nhất và khác 0.

Do đó nó là bội chung nhỏ nhất của 6 và 10 hay BCNN(6, 10) = 30.

d) Các bội chung của 6 và 10 là các bội của BCNN(6, 10) = 30. 

Mà các bội của 30 là: 0; 30; 60; 90; 120; 150; 180;…. (lần lượt nhân 30 với 0, 1, 2, …)

Vậy các bội chung của 6 và 10 nhỏ hơn 160 là: 0; 30; 60; 90; 120; 150.

Bài 3: Tìm bội chung nhỏ nhất của:

a) 7 và 13;

b) 54 và 108;

c) 21, 30, 70.

Trả lời rút gọn: 

a) BCNN(7, 13) = 7 . 13 = 91. 

b) BCNN(54, 108) = 2² . 3³ = 4 . 27 = 108.

c) BCNN(21, 30, 70) = 2 . 3. 5 . 7 = 210. 

Bài 4: Thực hiện phép tính sau...

Trả lời rút gọn: 

a) BCNN(48, 40) = 2⁴ . 3 .5 = 16 . 3 . 5 = 240.

+ 240 : 48 = 5; 240 : 40 = 6 

+ Ta có: 

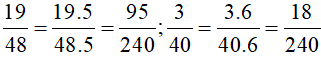
Vậy 

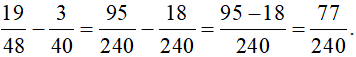
b) Để thực hiện phép tính, trước hết tìm bội chung nhỏ nhất của 6, 27 và 18 để quy đồng mẫu số.

+ Ta có: 6 = 2 . 3; 27 = 3³; 18 = 2 . 9 = 2 . 3² 

Các thừa số nguyên tố chung và riêng của 6, 27 và 18 là 2; 3, tương ứng với các số mũ lớn nhất là 1; 3. 

Khi đó: BCNN(6, 27, 18) = 2¹. 3³ = 2 . 27 = 54

+ 54 : 6 = 9; 54 : 27 = 2; 54 : 18 = 3

+ Ta có: 

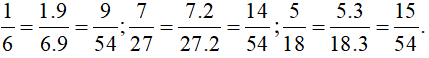
Vậy 

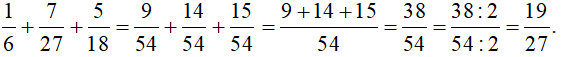
Bài 5: Bội chung nhỏ nhất của hai số là 45. Một trong hai số đó là 5. Hãy tìm số còn lại.

Trả lời rút gọn: 

Gọi số cần tìm là x

Ta có: BCNN(x, 5) = 45 

Mà 45 = 5 . 9 = 5 . 3² ; 5 = 5¹ và 5 là số nguyên tố nên x và 5 phải là hai số nguyên tố cùng nhau. 

Do đó x = 3² = 9.  

Vậy số cần tìm là 9. 

Bài 6: Câu lạc bộ thể thao của một trường trung học cơ sở có không quá 50 học sinh tham gia. Biết rằng khi chia số học sinh trong câu lạc bộ đó thành từng nhóm 5 học sinh hoặc 8 học sinh thì vừa hết. Câu lạc bộ thể thao đó có bao nhiêu học sinh? 

Trả lời rút gọn: 

Gọi a là số học sinh của câu lạc bộ thể thao (a ∈ , a ≤ 50)

Mà bội chung của 5 và 8 là các bội của BCNN(5, 8) = 40 

Nên BC(5, 8) ={0; 40; 80; 120; …}

Vì a ≤ 50 nên a = 40. 

Vậy câu lạc bộ thể thao đó có 40 học sinh. 

Bài 7: Lịch cập cảng của ba tàu như sau: tàu thứ nhất cứ 10 ngày cập cảng một lần; tàu thứ hai cứ 12 ngày cập cảng một lần; tàu thứ ba cứ 15 ngày cập cảng một lần. Vào một ngày nào đó, ba tàu cùng cập cảng. Sau ít nhất bao nhiêu ngày thì ba tàu lại cùng cập cảng?

Trả lời rút gọn: 

Sau ít nhất 60 ngày thì ba tàu lại cùng nhau cập cảng. 

CÓ THỂ EM CHƯA BIẾT

Lịch can Chi

Một số nước phương Đông, trong đó có Việt Nam, gọi tên năm âm lịch bằng cách ghép tên của một trong 10 can (theo thứ tự là Giáp, Ất, Bính, Đinh, Mậu, Kỷ, Canh, Tân, Nhâm, Quý) với tên của một trong 12 chi (theo thứ tự là Tỷ, Sửu, Dần, Mão, Thìn, Tỵ, Ngọ, Mùi, Thân, Dậu, Tuất, Hợi). Đầu tiên, Giáp được ghép với Tý thành năm Giáp Tý. Cứ 10 năm, Giáp được lặp lại. Cứ 12 năm, Tý được lặp lại:

Giải thích tại sao cứ 60 năm thì năm Giáp Tý được lặp lại?

Trả lời rút gọn: 

Cứ sau 60 năm thì năm Giáp Tý được lặp lại.