Slide bài giảng toán 6 cánh diều bài 5: Phép Nhân Các Số Nguyên (2 Tiết)

Tóm lược nội dung

CHƯƠNG II: SỐ NGUYÊN

BÀI 5: PHÉP NHÂN CÁC SỐ NGUYÊN

1. PHÉP NHÂN HAI SỐ NGUYÊN KHÁC DẤU

Bài 1: 

a) Hoàn thành phép tính: (– 3) . 4 = (– 3) + (– 3) + (– 3) + (– 3) = (?).

b) So sánh (– 3). 4 và – (3. 4).

Trả lời rút gọn:

a) Ta có: 

(– 3) . 4 = (– 3) + (– 3) + (– 3) + (– 3) = (– 6) + (– 3) + (– 3) = (– 9) + (– 3) = – 12.  

b) Theo câu a) ta có: (– 3) . 4 = – 12

Lại có: – (3 . 4) = – 12

Do đó: (– 3) . 4 = – (3 . 4). 

Bài 2: Tính:

a) (– 7) . 5;

b) 11 . (– 13).

Trả lời rút gọn:

a) (– 7) . 5 = – (7 . 5) = – 35.

b) 11 . (– 13) = – (11 . 13) = – 143. 

2. PHÉP CỘNG HAI SỐ NGUYÊN CÙNG DẤU

Bài 1: 

a) Quan sát kết quả của ba tích đầu, ở đó mỗi lần ta giảm 1 đơn vị ở thừa số thứ hai. Tìm kết quả của hai tích cuối.

(– 3) . 2 = – 6

(– 3) . 1 = – 3 tăng 3 đơn vị

(– 3) . 0 = 0 tăng 3 đơn vị

(– 3) . (–1) = (?₁) tăng 3 đơn vị

(– 3) . (– 2) = (?₂) tăng 3 đơn vị

b) So sánh (– 3). (– 2) và 3. 2.

Trả lời rút gọn: 

a) Số cần điền ở (?₁) là 3 (do tăng 3 đơn vị nên ta lấy 0 + 3 = 3)

Tương tự, số cần điền ở (?₂) là 6 (vì 3 + 3 = 6) 

Vậy ta đã tìm được kết quả hai tích cuối lần lượt là 3 và 6. 

b) Theo câu a ta có: (– 3) . (– 2) = 6 

Lại có:  3 . 2 = 6 

Do đó: (– 3) . (– 2) = 3 . 2

Bài 2: Tính giá trị của biểu thức trong mỗi trường hợp sau:

a) – 6x – 12 với x = – 2;

b) – 4y + 20 với y = – 8.

Trả lời rút gọn: 

a) Với x = – 2 thì ta có:

– 6x – 12 = (– 6) . (– 2) – 12 = 6 . 2 – 12 = 12 – 12 = 0.

b) Với y = – 8 thì ta có:

– 4y + 20 = (– 4) . (– 8) + 20 = 4 . 8 + 20 = 32 + 20 = 52. 

3. TÍNH CHẤT CỦA PHÉP NHÂN CÁC SỐ NGUYÊN

Bài 1: Tính và so sánh kết quả:

a) (– 4) . 7 và 7 . (– 4); 

b) [(– 3). 4] . (– 5) và (– 3) . [4. (– 5)];

c) (– 4) . 1 và – 4; 

d) (– 4) . (7 + 3) và (– 4) . 7 + (– 4) . 3.

Trả lời rút gọn: 

a) (– 4) . 7 = – (4 . 7) = – 28

7 . (– 4) = – (7 . 4) = – 28

Vậy (– 4) . 7 = 7 . (– 4).

b) [(– 3) . 4] . (– 5) = [– (3 . 4)] . (– 5) = (– 12) . (– 5) = 60

(– 3) . [4 . (– 5)] = (– 3) . [– (4 . 5)] = (– 3) . (– 20) = 60

Do đó: [(– 3) . 4] . (– 5) = (– 3) . [4 . (– 5)].

c) (– 4) . 1 = – (4 . 1) = – 4

Vậy (– 4) . 1 = – 4.

d) (– 4) . (7 + 3) = (– 4) . 10 = – (4 . 10) = – 40

(– 4) . 7 + (– 4) . 3 = [– (4 . 7)] + [– (4 . 3)] = (– 28) + (– 12) = – (28 + 12) = – 40

Vậy (– 4) . (7 + 3) = (– 4) . 7 + (– 4) . 3. 

Bài 2: Tính một cách hợp lí:

a) (– 6) . (– 3) . (– 5);

b) 41 . 81 – 41. (– 19).

Trả lời rút gọn: 

a) (– 6) . (– 3) . (– 5) 

= [(–6) . (– 5)] . (– 3)                 (tính chất giao hoán và kết hợp)

= 30 . (– 3) 

= – 90. 

b) 41 . 81 – 41 . (– 19) 

= 41 . [81 – (– 19)]          (tính chất phân phối của phép nhân đối với phép trừ)

= 41 . (81 + 19) 

= 41 . 100

= 4 100. 

`BÀI TẬP

Bài 1: Tính:

a) 21 . (– 3); 

b) (– 16) . 5; 

c) 12 . 20; 

d) (– 21) . (– 6).

Trả lời rút gọn: 

a) 21 . (– 3) = – (21 . 3) = – 63. 

b) (– 16) . 5 = – (16 . 5) = – 80.

c) 12 . 20 = 240.

d) (– 21) . (– 6) = 21 . 6 = 126. 

Bài 2: Tìm số thích hợp ở (?):

Trả lời rút gọn: 

Ta có: 15 . 6 = 90 

(– 3) . 14 = – (3 . 14) = – 42

11 . (– 23) = – (23 . 11) = – 253

(– 4) . (– 125) = 4 . 125 = 500 

Có: 21 = 7 . 3 nên 21 . (– 1) = 7 .  3 . (– 1) hay – 21 = 7 . (– 3) 

72 = 9 . 8 = (– 9) . (– 8) 

Khi đó các số thích hợp được điền vào bảng như sau: 

Bài 3: Tính:

a) 10¹⁰ . (– 10⁴), 

b) (– 2) . (– 2) . (– 2) . (– 2) . (– 2) + 2⁵;

c) (– 3) . (– 3) . (– 3) . (– 3) – 3⁴.

Trả lời rút gọn: 

a) 10¹⁰ . (– 10⁴) = – (10¹⁰ . 10⁴) = – (10^{10 + 4})  = – 10¹⁴. 

b) (– 2) . (– 2) . (– 2) . (– 2) . (– 2) + 2⁵

= – (2 . 2 . 2 . 2 . 2) + 2⁵ 

= [– (2)⁵] + 2⁵ 

= 2⁵ – 2⁵

= 0. 

c) (– 3) . (– 3) . (– 3) . (– 3) – 3⁴.

= 3 . 3 . 3. 3 – 3⁴

= 3⁴ – 3⁴ 

= 0. 

Bài 4: Tính 8. 25. Từ đó suy ra kết quả của các phép tính sau:

a) (– 8) . 25;

b) 8 . (– 25);

c) (– 8) . (– 25).

Trả lời rút gọn: 

Ta có: 8 . 25 = 200 

Do đó ta suy ra được: 

a) (– 8) . 25 = – (8 . 25) = – 200;

b) 8 . (– 25) = – (8 . 25) = – 200;

c) (– 8) . (– 25) = 8 . 25 = 200.

Bài 5: Tính giá trị của biểu thức trong mỗi trường hợp sau:

a) 2x, biết x = – 8; 

b) – 7y, biết y = 6; 

c) – 8z – 15, biết z = – 4.

Trả lời rút gọn: 

a) Với x = – 8 thì ta có: 

2x = 2 . (– 8) = – (2 . 8) = – 16.

b) Với y = 6 thì ta có:

– 7y = (– 7) . 6 = – (7 . 6) = – 42. 

c) Với z = – 4 thì ta có: 

– 8z – 15 = (– 8) . (– 4) – 15 = 8 . 4 – 15 = 32 – 15 = 17. 

Bài 6: Xác định các dấu “ < “, “>” thích hợp cho (?)...

Trả lời rút gọn: 

a) Ta có: 3 . (– 5) = – (3 . 5) = – 15 < 0 

Do đó: 3 . (– 5) 0.

b) Ta có: (– 3) . (– 7) = 3 . 7 = 21 > 0

Vậy (– 3) . (– 7) 0. 

c) Ta có: (– 6) . 7 = – (6 . 7) = – 42 < 0

(– 5) . (– 2) = 5 . 2 = 10 > 0

Do đó: – 42 < 10 

Vậy (– 6) . 7 (– 5) . (– 2).

Bài 7: Tính một cách hợp lí:

a) (– 16) . (– 7) . 5; 

b) 11. (– 12) + 11. (– 18);

c) 87. (– 19) – 37 . (– 19); 

d) 41 . 81 .(– 451). 0.

Trả lời rút gọn: 

a) (– 16) . (– 7) . 5 

= [(– 16) . 5] . (– 7)          (tính chất giao hoán và kết hợp)

= [– (16 . 5)] . (– 7) 

= (– 80) . (– 7)

= 80 . 7 

= 560. 

b) 11 . (– 12) + 11 . (– 18) 

= 11 . [(– 12) + (– 18)]     (tính chất phân phối của phép nhân đối với phép cộng)

= 11 . [– (12 + 18)] 

= 11 . (– 30) 

= – (11 . 30) 

= – 330.  

c) 87 . (– 19) – 37 . (– 19) 

= (– 19) . (87 – 37)          (tính chất phân phối của phép nhân đối với phép trừ)

= (– 19) . 50 

= – (19 . 50)

 = – 950. 

d) 41 . 81 . (– 451) . 0 = 0.         (tính chất phép nhân một số với 0) 

Hoặc chúng ta có thể làm lần lượt từng bước như sau: 

41 . 81 . (– 451) . 0 

= 41 . 81 . [(– 451) . 0]     (tính chất kết hợp)

= 41 . 81 . 0           (tính chất phép nhân một số với 0)

= 41 . (81 . 0)         (tính chất kết hợp)

= 41 . 0 = 0.           (tính chất phép nhân một số với 0)

Bài 8: Chọn từ “âm”, “dương” thích hợp cho (?)

a) Tích ba số nguyên âm là một số nguyên (?);

b) Tích hai số nguyên âm với một số nguyên dương là một số nguyên (?);

c) Tích của một số chẵn các số nguyên âm là một số nguyên (?);

d) Tích của một số lẻ các số nguyên âm là một số nguyên (?).

Trả lời rút gọn: 

a) Ta có: tích của hai số nguyên âm là một số nguyên dương

Do đó tích của ba số nguyên âm (chính là tích của hai số nguyên âm với một số nguyên âm) là một số nguyên âm. 

b) 

Nên tích của hai số nguyên âm với một số nguyên dương (chính là tích của hai số nguyên dương) là một số nguyên dương. 

c) Tích của hai số nguyên âm là một số nguyên dương

Vậy tích của một số chẵn các số nguyên âm là một số nguyên dương. 

d) Tích của ba số nguyên âm là một số nguyên âm (câu a)

Vậy tích của một số lẻ các số nguyên âm là một số nguyên âm. 

Bài 9: Công ty Ánh Dương có lợi nhuận ở mỗi tháng trong Quý I là – 30 triệu đồng. Trong Quý II, lợi nhuận mỗi tháng của công ty là 70 triệu đồng. Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là bao nhiêu tiền?

Trả lời rút gọn: 

Cách 1. 

Mỗi quý thì có 3 tháng. 

Lợi nhuận của công ty trong Quý I là: 

(– 30) . 3 = – 90 (triệu đồng)

Lợi nhuận của công ty trong Quý II là:

70 . 3 = 210 (triệu đồng)

Lợi nhuận của công ty Ánh Dương trong 6 sáu đầu năm (2 quý đầu năm) là:

(– 90) + 210 = 120 (triệu đồng)

Vậy sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là 120 triệu đồng. 

Cách 2. (làm gộp)

Mỗi quý có 3 tháng nên lợi nhuận của công ty Ánh Dương trong 6 tháng đầu năm là: 

(– 30) . 3 + 70 . 3 = 3 . [(– 30) + 70] = 120 (triệu đồng)

Vậy sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là 120 triệu đồng. 

Bài 10: Sử dụng máy tính cầm tay

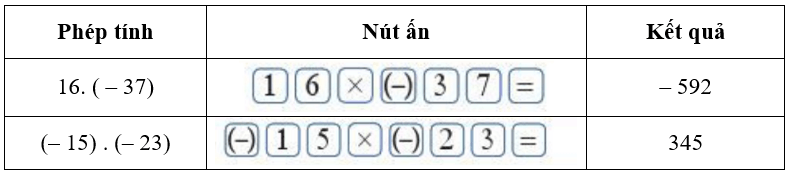
Dùng máy tính cầm tay để tính:

23 . (– 49); 

(– 215) . 207; 

(– 124) . (– 1 023).

Trả lời rút gọn: 

23 . (– 49) = – 1 127; 

(– 215) . 207 = – 44 505;  

(– 124) . (– 1 023) = 126 852.