Slide bài giảng toán 6 cánh diều bài 2: Hai đường thẳng cắt nhau. Hai đường thẳng song song

Tóm lược nội dung

CHƯƠNG 6. HÌNH HỌC PHẲNG

BÀI 2: HAI ĐƯỜNG THẲNG CẮT NHAU. HAI ĐƯỜNG THẲNG SONG SONG

1. HAI ĐƯỜNG THẲNG CẮT NHAU

Bài 1: Hai đường thẳng ở Hình 26 có bao nhiêu điểm chung?

Trả lời rút gọn:

Hai đường thẳng ở Hình 26 có 1 điểm chung duy nhất là O.

Bài 2: 

a) Vẽ đường thẳng d đi qua hai điểm A và B.

b) Đường thẳng d có cắt đường thẳng c hay không?

Trả lời rút gọn:

a) Dùng thước thẳng vẽ đường thẳng đi qua hai điểm A và B như hình vẽ:

b) Đường thẳng d cắt đường thẳng c tại điểm M:

Bài 3: Cho ba điểm M, N, P như Hình 30.

a) Vẽ đường thẳng NP.

b) Vẽ hai đường thẳng đi qua M và cắt đường thẳng NP.

Trả lời rút gọn:

a) Đường thẳng NP:

b) Ta có thể vẽ được vô số đường thẳng qua M cắt đường thẳng NP:

2. HAI ĐƯỜNG THẲNG SONG SONG

Bài 1: Mỗi bức ảnh sau đây gợi nên hình ảnh về hai đường thẳng. Hai đường thẳng đó có điểm chung không?

Trả lời rút gọn:

Hình ảnh các con đường nhìn từ trên cao là các đường thẳng không có điểm chung.

Hình ảnh hai đường dây điện trên bầu trời là các đường thẳng không có điểm chung.

Bài 2: Quan sát Hình 34

a) Chỉ ra các cặp đường thẳng song song.

b) Chỉ ra các cặp đường thẳng cắt nhau.

Trả lời rút gọn:

a) Các cặp đường thẳng song song là: a và d, b và c.

b) Các cặp đường thẳng cắt nhau là: a và b, a và c, b và d, c và d.

BÀI TẬP

Bài 1: Quan sát Hình 35, đọc tên hai đường thẳng song song, hai đường thẳng cắt nhau và chỉ ra giao điểm của chúng (nếu có).

Trả lời rút gọn:

- Hai đường thẳng song song là a và b.

- Hai đường thẳng cắt nhau là m và n với giao điểm là T.

- Hai đường thẳng cắt nhau là b và c với giao điểm là H.

Bài 2: Quan sát Hình 36 và chỉ ra:

a) Các cặp đường thẳng song song.

b) Các cặp đường thẳng cắt nhau.

Trả lời rút gọn:

a) Các cặp đường thẳng song song:

a và b, b và c, a và c, d và e.

b) Các cặp đường thẳng cắt nhau:

a và d, a và e, b và d, b và e, c và d, c và e.

Bài 3: 

Trả lời rút gọn:

Đặt tên các đường thẳng cắt nhau:

Đường thẳng a và đường thẳng c với giao điểm là A;

Đường thẳng a và đường thẳng d với giao điểm là B;

Đường thẳng b và đường thẳng d với giao điểm là D;

Đường thẳng b và đường thẳng c với giao điểm là E;

Đường thẳng c và đường thẳng d với giao điểm là C.

Bài 4: Cho ba điểm H, I, K thẳng hàng.

a) Điểm K có thuộc đường thẳng IH không?

b) Vẽ đường thẳng d đi qua H và không đi qua I. Đường thẳng d có song song với đường thẳng IK không?

Trả lời rút gọn:

a) Qua hai điểm I và H ta chỉ vẽ được duy nhất một đường thẳng đi qua hai điểm này.

Mà ba điểm H, I, K thẳng hàng nên K phải thuộc đường thẳng IH.

Vậy điểm K thuộc đường thẳng IH.

b) Vì ba điểm H, I, K thẳng hàng nên đường thẳng IK đi qua điểm H, mà đường thẳng d cũng đi qua điểm H nên hai đường thẳng này có điểm chung là H. Do đó đường thẳng d không song song với đường thẳng IK.

Bài 5: Cho ba điểm P, Q, R không thẳng hàng. Vẽ các đường thẳng đi qua hai trong ba điểm đã cho.

a) Điểm P là giao điểm của hai đường thẳng nào?

b) Chỉ ra các cặp đường thẳng cắt nhau.

Trả lời rút gọn:

a) Ta vẽ đường thẳng a đi qua hai điểm P và Q; đường thẳng b đi qua hai điểm Q và R, đường thẳng c đi qua hai điểm P và R.

Ta thấy điểm P là giao điểm của hai đường thẳng a và c.

b) Các cặp đường thẳng cắt nhau là:

Đường thẳng a và đường thẳng b với giao điểm là Q;

Đường thẳng a và đường thẳng c với giao điểm là P;

Đường thẳng b và đường thẳng c với giao điểm là R.

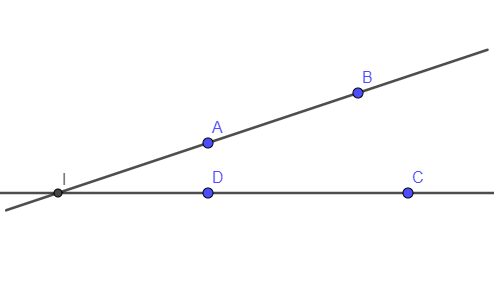
Bài 6: Vẽ hình theo cách diễn đạt sau:

a) Đường thẳng AB và đường thẳng CD cắt nhau tại I.

b) Hai đường thẳng a và b cắt nhau tại O, đường thẳng c cắt a tại P và cắt b tại Q.

Trả lời rút gọn:

a) 

– Chấm bốn điểm A, B, C và D (sao cho 4 điểm này không cùng nằm trên một đường thẳng)

- Ta vẽ đường thẳng AB đi qua hai điểm A và B, vẽ đường thẳng CD đi qua hai điểm C và D. Hai đường thẳng này cắt nhau tại I.

b)

- Vẽ hai đường thẳng a và b bất kì cắt nhau tại O.

- Vẽ đường thẳng c cắt a tại P và cắt b tại Q