Slide bài giảng Toán 12 kết nối Hoạt động thực hành trải nghiệm: Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình thang

Tóm lược nội dung

TÍNH NGUYÊN HÀM VÀ TÍCH PHÂN VỚI PHẦN MỀM GEOGEBRA

TÍNH GẦN ĐÚNG TÍCH PHÂN BẰNG PHƯƠNG PHÁP HÌNH THANG

1. Tính nguyên hàm và tích phân với phần mềm GeoGebra

Thực hành 1.

Sử dụng phần mềm GeoGebra, tính:

a)

b)

Trả lời rút gọn:

Khởi động phần mềm GeoGebra, chọn Complex Adaptive System (CAS) để thực hiện tính toán nguyên hàm và hàm số.

a) Để tính nguyên hàm của hàm số, ta dùng lệnh IntegralSymbolic(Function) (IntegralSymbolic(<hàm số>)), kết quả sẽ được hiển thị ngay bên dưới:

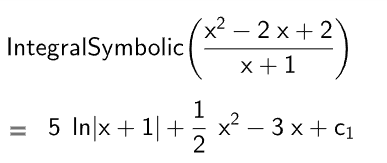
b)

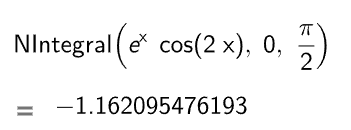
2. Tính gần đúng tích phân bằng phương pháp hình thang

Thực hành 2. Sử dụng phương pháp hình thang, tính gần đúng với độ chính xác 0,01.

Trả lời rút gọn:

Bước 1: Tính và tìm

Do đó

Bước 2: Với sai số cho trước, tìm số tự nhiên (nhỏ nhất) sao cho:

Như vậy, ta cần tìm sao cho:

Do đó, ta chọn 5

Bước 3: Chia đoạn thành n đoạn con có độ dài bằng nhau và áp dụng công thức tính diện tích hình thang

Chia đoạn thành 5 đoạn con có độ dài bằng nhau là

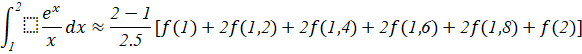
Vận dụng. Một thân cây dài 4,8 m được cắt thành các khúc gỗ dài 60 cm. Người ta đo đường kính của mỗi mặt cắt ngang và diện tích S của nó được ghi lại trong bảng dưới đây, ở đây x (cm) là khoảng cách tính từ đỉnh thân cây đến vết cắt.

Tìm thể tích gần đúng của thân cây này.

Trả lời rút gọn:

, trong đó là diện tích mặt cắt ngang tại vị trí cách đỉnh thân cây một khoảng (cm).

Thân cây dài 4,8 m được chia thành 8 khúc có độ dài 60 cm là: , , , , , , ,

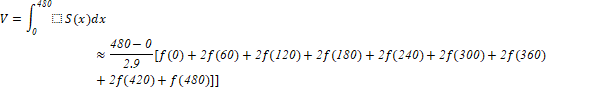
Vậy thân cây có thể tích gần đúng là .