Slide bài giảng Toán 12 kết nối Bài 11: Nguyên hàm

Tóm lược nội dung

BÀI 11: NGUYÊN HÀM

1. Nguyên hàm của 1 hàm số

Hoạt động 1: Cho hai hàm số và , với

a) Tính đạo hàm của hàm số .

b) và có bằng nhau không?

Trả lời rút gọn:

a)  .

b) .

Luyện tập 1: Hàm số nào dưới đây là một nguyên hàm của hàm số trên khoảng ?

a) ;                   b) .

Trả lời rút gọn:

, .

Vì với mọi nên hàm số là một nguyên hàm của trên

Hàm số không là nguyên hàm của trên vì với

.

Hoạt động 2: Nhận biết họ nguyên hàm của một hàm số

a) Chứng minh rằng hàm số là một nguyên hàm của hàm số trên .

b) Hàm số (với C là hằng số) có là một nguyên hàm của hàm số trên không? Vì sao?

Trả lời rút gọn:

a) . 

Vì với mọi nên hàm số là một nguyên hàm của trên .

b) 

Vì với mọi nên hàm số là một nguyên hàm của trên .

Luyện tập 2: Tìm .

Trả lời rút gọn:

.

2. Tính chất cơ bản của nguyên hàm

Hoạt động 3: Khám phá nguyên hàm của tích một hàm số với một hằng số khác 0

Cho là hàm số liên tục trên , là một hằng số khác 0. Giả sử là một nguyên hàm của trên .

a) Chứng minh là một nguyên hàm của hàm số trên .

b) Nêu nhận xét về và .

Trả lời rút gọn:

a) Do là một nguyên hàm của trên nên .

.

là một nguyên hàm của hàm số trên .

b) ; .

 .

Luyện tập 3: Cho hàm số (*).

a) Chứng minh rằng hàm số là một nguyên hàm của hàm số . Từ đó tìm .

b) Từ kết quả câu a, tìm ( là hằng số thực khác 0).

Trả lời rút gọn:

a)  

là một nguyên hàm của hàm số .

.

b) .

Hoạt động 4: Khám phá nguyên hàm của một tổng

Cho và là hai hàm số liên tục trên . Giả sử là một nguyên hàm của , là một nguyên hàm của trên .

a) Chứng minh là một nguyên hàm của hàm số trên .

b) Nêu nhận xét về và .

Trả lời rút gọn:

a) Vì nên là một nguyên hàm của hàm số trên .

b) ,

      .

Vậy .

Luyện tập 4: Tìm:

a) ;

b) .   

Trả lời rút gọn:

a) .             

b) .                         

Vận dụng: Doanh thu bán hàng của một công ty khi bán một loại sản phẩm là số tiền (triệu đồng) thu được khi đơn vị sản phẩm được bán ra. Tốc độ biến động (thay đổi) của doanh thu khi đơn vị sản phẩm đã được bán ra là hàm số . Một công ty công nghệ cho biết, tốc độ biến đổi của doanh thu khi bán một loại con chíp của hãng được cho bởi , ở đó là số lượng chíp đã bán. Tìm doanh thu của công ty khi đã bán 1000 con chíp.

Trả lời rút gọn:

Vì nên doanh thu là một nguyên hàm của .

.

  nên và  (triệu đồng).

Khi bán 1000 con chíp nên (triệu đồng).

3, Nguyên hàm của một số hàm số thường gặp

a) Nguyên hàm của hàm số lũy thừa

Hoạt động 5: Khám phá nguyên hàm của hàm số lũy thừa

a) Với , tính đạo hàm của hàm số ().

b) Cho hàm số (). Tính đạo hàm của hàm số này trong hai trường hợp: và .

Trả lời rút gọn:

a) .

b) Trường hợp 1: ,

    Trường hợp 2: x < 0,

+ Đặt , ta có

+ Khi đó .

Luyện tập 5: Tìm:

a) ;

b) ();

c) ().

Trả lời rút gọn:

a)

b)

c)

b) Nguyên hàm của hàm số lượng giác

Hoạt động 6: Khám phá nguyên hàm của hàm số lượng giác

a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.

Trả lời rút gọn:

a) 

b)

Luyện tập 6: Tìm :

a) ;

b) .

Trả lời rút gọn:

a)

                                           .

b)

                                       .

c) Nguyên hàm của số mũ

Hoạt động 7: Khám phá nguyên hàm của số mũ

a) Tính đạo hàm của các hàm số sau và kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.

Trả lời rút gọn:

a)

b)

Luyện tập 7: Tìm:

a) ;

b) ;

c) .

Trả lời rút gọn:

a) .

b) .

c)

GIẢI BÀI TẬP

Bài 4.1:Trong mỗi trường hợp sau, hàm số có là một nguyên hàm của hàm số trên khoảng tương ứng không? Vì sao?

a) và trên khoảng ;

b) và trên .

Trả lời rút gọn:

a)

Vì nên là một nguyên hàm của trên khoảng .

b) Đặt , ta có

.

Vì nên không phải một nguyên hàm của trên .

Bài 4.2 :Tìm nguyên hàm của các hàm số sau:

a) ;

b) ;

c) ;

d) .

Trả lời rút gọn:

a) .

b) .

c)

                              .

d)

 .

Bài 4.3 :Tìm:

a) ;

b) với ;

c) ;

d) .

Trả lời rút gọn:

a)

                                  .

b)

                                    .

c)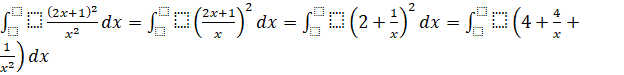

                         .

d) .

Bài 4.4:Tìm:

a) ;

b) ;

c) ;

d) .

Trả lời rút gọn:

a) .

b) .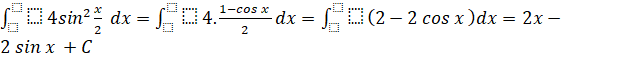

c)

                                        .

d)    

Bài 4.5 :Cho hàm số xác định trên khoảng . Biết rằng, với mọi và . Tính giá trị .

Trả lời rút gọn:

;

Mà nên

  ⇒ .

Bài 4.6 : Cho hàm số có đồ thị là . Xét điểm thay đổi trên . Biết rằng hệ số góc của tiếp tuyến của đồ thị tại là và điểm trùng với gốc tọa độ khi nó nằm trên trục tung. Tìm biểu thức .

Trả lời rút gọn:

Vì là hệ số góc của tiếp tuyến đồ thị nên . Do đó là một nguyên hàm của , ta có:

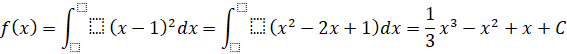
Điểm trùng gốc tọa độ khi nó nằm trên trục tung nên nên .

 .

Bài 4.7 :Một viên đạn được bắn thẳng đứng lên trên từ mặt đất. Giả sử tại thời điểm giây (coi là thời điểm viên đạn được bắn lên), vận tốc của nó được cho bởi (m/s). Tìm độ cao của viên đạn (tính từ mặt đất):

a) Sau giây;

b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất).

Trả lời rút gọn:

a) Gọi là độ cao viên đạn đạt được sau giây kể từ lúc viên đạn được bắn lên.

 . 

là một nguyên hàm số của , ta có:

.

Theo giả thiết, nên và ta được (m).

giây => (m).

b)Viên đạn đạt độ cao lớn nhất khi vận tốc .

⇒ (giây).

Vậy độ cao lớn nhất viên đạn đạt được là (m).