Slide bài giảng Toán 12 kết nối Bài 15: Phương trình đường thẳng trong không gian

Tóm lược nội dung

BÀI 15: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN

1. Phương trình đường thẳng

a) Vecto chỉ phương của đường thẳng

Hoạt động 1. Hình thành khái niệm vectơ chỉ phương của đường thẳng

Trong không gian, cho điểm M và vectơ  khác vectơ – không. Khẳng định nào trong hai khẳng định sau là đúng?

a) Có duy nhất đường thẳng đi qua M và vuông góc với giá của  .

b) Có duy nhất đường thẳng đi qua M và song song hoặc trùng với giá của  .

Trả lời rút gọn:

b) đúng

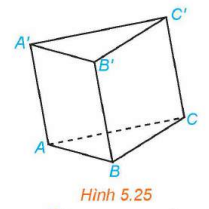
Luyện tập 1: Cho hình lăng trụ (H.5.25). Trong các vectơ có điểm đầu và điểm cuối đều là đỉnh của hình lăng trụ, những vectơ nào là vectơ chỉ phương của đường thẳng ?

Trả lời rút gọn:

Những vectơ nào là vectơ chỉ phương của đường thẳng là:

b) Phương trình tham số của đường thẳng

Hoạt động 2. Hình thành khái niệm phương trình tham số của đường thẳng

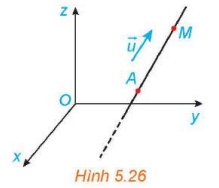
Trong không gian , một vật thể chuyển động với vectơ vận tốc không đổi  và xuất phát từ điểm (H.5.26).

a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm mà nó đi qua và vectơ chỉ phương của đường thẳng đó)? 

b) Giả sử tại thời điểm tính từ khi xuất phát, vật thể ở vị trí . Tính theo và .

Trả lời rút gọn:

a) 

Vật thể chuyển động trên đường thẳng qua A và song song với giá của vectơ  

b) Tại thời điểm tính từ khi xuất phát, vật thể ở vị trí nên:

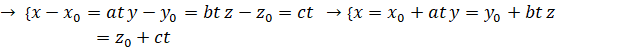
Luyện tập 2. Trong không gian Oxyz, cho đường thẳng : 

a) Hãy chỉ ra hai điểm thuộc và một vectơ chỉ phương của ∆.

b) Viết phương trình tham số của đường thẳng đi qua gốc toạ độ và có vectơ chỉ phương

Trả lời rút gọn:

a) Do có phương trình  nên điểm và điểm thuộc và là một vecto chỉ phương của .

b) Đường thẳng có phương trình:

c) Phương trình chính tắc của đường thẳng

Hoạt động 3. Hình thành khái niệm phương trình chính tắc của đường thẳng

Trong không gian , cho đường thẳng đi qua điểm và có vectơ chỉ phương (a, b, c là các số khác 0).

a) Điểm thuộc khi và chỉ khi hai vectơ và có mối quan hệ gì?

b) Điểm thuộc khi và chỉ khi các phân số có mối quan hệ gì?

Trả lời rút gọn:

a) Điểm thuộc  

⇔và cùng phương

b) Đường thẳng có phương trình:

Điểm thuộc nên toạ độ của M thoả mãn:

Luyện tập 3: Trong không gian , cho đường thẳng . Hãy chỉ ra một vecto chỉ phương của và 2 điểm thuộc

Trả lời rút gọn:

Đường thẳng có phương trình nên và thuộc và là một vecto chỉ phương của .

Luyện tập 4: Trong không gian , viết phương trình tham số và phương trình chính tắc của đường thẳng đi qua điểm và có vectơ chỉ phương

Trả lời rút gọn:

Phương trình tham số của

Phương trình chính tắc của

Luyện tập 5: Trong không gian , viết phương trình tham số của đường thẳng đi qua điểm và vuông góc với mặt phẳng

Trả lời rút gọn:

Mặt phẳng có một vectơ pháp tuyến là . Giá của và cùng vuông góc với nên chúng trùng nhau hoặc song song với nhau.

Do đó nhận làm một vecto chỉ phương.

Vậy phương trình tham số của đường thẳng là:

d) Lập phương trình đường thẳng đi qua hai điểm

Hoạt động 4: Lập phương trình đường thẳng đi qua hai điểm

Trong không gian , cho hai điểm phân biệt

a) Hãy chỉ ra một vecto chỉ phương của đường thẳng

b) Viết phương trình đường thẳng

Trả lời rút gọn:

a) Một vecto chỉ phương của đường thẳng là

b) Đường thẳng đi qua điểm và có nên có:

Phương trình tham số là:

Phương trình chính tắc là:  với điều kiện

Luyện tập 6: Trong không gian , viết phương trình đường thẳng đi qua hai điểm

Trả lời rút gọn:

Đường thẳng đi qua điểm nên có vecto chỉ phương

  có phương trình tham số là: và không có phương trình chính tắc do

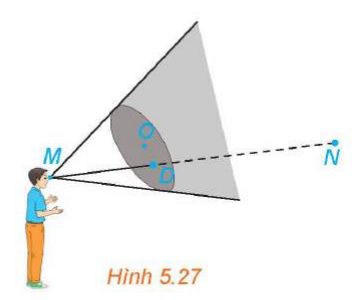
Vận dụng 1: (H.5.27) Trong tình huống mở đầu hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra.

Trong không gian , mắt một người quan sát đặt ở điểm và vật cần quan sát đặt tại điểm ). Một tấm bìa chắn đường truyền của ánh sáng có dạng hình tròn với tâm , bán kính bằng 3 và đặt trong mặt phẳng . Hỏi tấm bìa có che khuất tầm nhìn của người quan sát đối với vật đặt ở điểm hay không?

a) Viết phương trình tham số của đường thẳng .

b) Tính toạ độ giao điểm của đường thẳng với mặt phẳng .

c) Hỏi điểm có nằm giữa hai điểm và hay không?

Trả lời rút gọn:

a) Đường thẳng đi qua và có vectơ chỉ phương nên có phương trình tham số là:

b) Vì thuộc mặt phẳng và đường thẳng nên

Mặt khác cũng thuộc đường thẳng

c)  

nằm giữa 2 điểm

Vậy tấm bìa có che khuất tầm nhìn của người quan sát đối với vật đặt ở điểm .

2. Hai đường thẳng vuông góc

Hoạt động 5. Tìm điều kiện để hai đường thẳng vuông góc

Trong không gian Oxyz, cho 2 đường thẳng tương ứng có vecto chỉ phương .

a) Hai đường thẳng và  vuông góc với nhau khi và chỉ khi 2 giá của có mối quan hệ gì?

b) Tìm điều kiện đối với  để và  vuông góc với nhau.

Trả lời rút gọn:

a) Hai đường thẳng và vuông góc với nhau khi và chỉ khi 2 giá của vuông góc với nhau

b) Nếu hai đường thẳng và vuông góc với nhau thì 2 giá của vuông góc với nhau. 

.

Luyện tập 7. Trong không gian , cho đường thẳng Hỏi đường thẳng có vuông góc với trục hay không?

Trả lời rút gọn:

Đường thẳng và trục Oz có vecto chỉ phương lần lượt là

Do nên đường thẳng không vuông góc với trục

Vận dụng 2: Tại một nút giao thông có hai con đường. Trên thiết kế, trong không gian , hai con đường đó tương ứng thuộc hai đường thẳng: 

Hỏi hai con đường trên có vuông góc với nhau hay không?

Trả lời rút gọn:

Các đường thẳng và có vecto chỉ phương lần lượt là

) nên hai đường thẳng và vuông góc với nhau

3. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG 

Hoạt động 6. Xác định vị trí tương đối giữa hai đường thẳng

Trong không gian Oxyz, cho hai đường thẳng và lần lượt đi qua các điểm và tương ứng có vecto chỉ phương phương (H.5.29).

a) Tìm điều kiện đối với để và song song hoặc trùng nhau.

b) Giả sử và  thì và có cắt nhau hay không?

c) Giả sử thì và có chéo nhau hay không?

Trả lời rút gọn:

a) Để và song song hoặc trùng nhau thì giá của 2 vecto song song hoặc trùng nhau.

Do đó 2 vecto cùng phương với nhau

b) Vì và  . 

=> và cắt nhau

c) Vì và chéo nhau

Luyện tập 8. Trong không gian , chứng minh hai đường thẳng sau song song với nhau:

và

Trả lời rút gọn:

Đường thẳng đi qua điểm và có vectơ chỉ phương

Đường thẳng đi qua điểm và có vectơ chỉ phương

Do và không thuộc ( nên hai đường thẳng và  song song với nhau

Luyện tập 9. Trong không gian , cho hai đường thẳng: và Chứng minh rằng:

a) Hai đường thẳng và  song song với nhau;

b) Đường thẳng và trục chéo nhau;

c) Đường thẳng trùng với đường thẳng

d) Đường thẳng cắt trục .

Trả lời rút gọn:

Đường thẳng đi qua điểm và có vectơ chỉ phương

Đường thẳng đi qua điểm và có vectơ chỉ phương

a) Do và không thuộc ( nên hai đường thẳng và  song song với nhau

b) Trục đi qua điểm và có vectơ chỉ phương

  và

  nên đường thẳng và trục chéo nhau

c) Đường thẳng đi qua điểm và có vectơ chỉ phương

Do và thuộc ( nên hai đường thẳng và  trùng nhau

d) Trục đi qua điểm và có vectơ chỉ phương

  và

Do và nên đường thẳng và trục cắt nhau

Luyện tập 10. Trong không gian Oxyz, xét vị trí tương đối giữa 2 đường thẳng:

Trả lời rút gọn:

Các đường thẳng và có vecto chỉ phương lần lượt là

không cùng phương

Xét hệ phương trình 2 ẩn t, s: (*)

Giải (1) và (2) ta được:

Thay vào (3) ta được:

→ Hệ phương trình (*) vô nghiệm 

Mà không cùng phương → và chéo nhau        

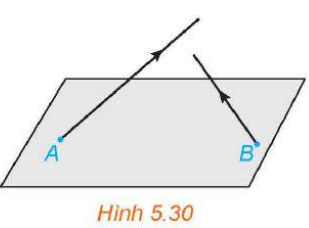
Vận dụng 3. (H.5.30) Trong không gian , có hai vật thể lần lượt xuất phát từ và với vận tốc không đổi tương ứng là Hỏi trong quá trình chuyển động, hai vật thể có va chạm vào nhau hay không?

Trả lời rút gọn:

Xét 2 đường thẳng và :

Đường thẳng đi qua điểm và có 

Đường thẳng đi qua điểm và có

  và

Do nên 2 đường thẳng và chéo nhau

Vậy trong quá trình chuyển động, hai vật thể không va chạm vào nhau

GIẢI BÀI TẬP

Bài 5.11 

Trong không gian , viết các phương trình tham số và chính tắc của đường thẳng đi qua và song song với đường thẳng : .

Trả lời rút gọn:

Đường thẳng có vecto chỉ phương Giá của và đường thẳng đều song song với nên chúng trùng nhau hoặc song song với nhau. 

Do đó đường thẳng nhận làm vecto chỉ phương

Mà thuộc nên có:

• Phương trình tham số:
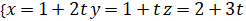
• Phương trình chính tắc:

Bài 5.12: Trong không gian , viết các phương trình tham số và chính tắc của đường thẳng đi qua và vuông góc với mặt phẳng

Trả lời rút gọn:

Mặt phẳng có một vectơ pháp tuyến là . Giá của và cùng vuông góc với nên chúng trùng nhau hoặc song song với nhau.

 Do đó nhận làm một vecto chỉ phương.

Mà thuộc nên có:

• Phương trình tham số:
• Phương trình chính tắc:

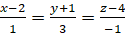
Bài 5.13: Trong không gian , viết các phương trình tham số và chính tắc của đường thẳng đi qua hai điểm

Trả lời rút gọn:

Đường thẳng đi qua điểm nên có vecto chỉ phương.

 Do đó có phương trình tham số là: và phương trình chính tắc là:

Bài 5.14: Trong không gian , cho hai đường thẳng:

và .

a) Chứng minh rằng và  cắt nhau

b) Viết phương trình mặt phẳng chứa và

Trả lời rút gọn:

a) Phương trình tham số của đường thẳng là: (*)

Giải (1) và (2) ta được:

Thay vào (3) ta được: (luôn đúng)

→ Hệ phương trình (*) có 1 nghiệm duy nhất

và  cắt nhau tại

b) Các đường thẳng và có vecto chỉ phương lần lượt là

Mặt phẳng chứa và nên nhận vecto làm vectơ pháp tuyến

Mặt phẳng chứa điểm và có vectơ pháp tuyến nên có phương trình là:

Bài 5.15: Trong không gian , cho hai đường thẳng:

  và

a) Chứng minh rằng và song song với nhau

b) Viết phương trình mặt phẳng chứa và

Trả lời rút gọn:

a) Đường thẳng đi qua điểm và có vectơ chỉ phương

Đường thẳng đi qua điểm và có vectơ chỉ phương

Do và không thuộc ( nên hai đường thẳng và  song song với nhau

b) Mặt phẳng chứa và nên nhận vecto làm vectơ pháp tuyến

Mặt phẳng chứa điểm và có vectơ pháp tuyến nên có

Bài 5.16: Trong không gian Oxyz, xác định vị trí tương đối giữa 2 đường thẳng:

Trả lời rút gọn:

Các đường thẳng và có vecto chỉ phương lần lượt là

không cùng phương (*)

Giải (1) và (2) ta được:

Thay vào (3) ta được:

→ Hệ phương trình (*) vô nghiệm 

Mà không cùng phương → và chéo nhau

Bài 5.17:Tại một nút giao thông có hai con đường. Trên thiết kế, trong không gian , hai con đường đó thuộc hai đường thẳng lần lượt có phương trình:

  và

a) Hai con đường trên có vuông góc với nhau hay không?

b) Nút giao thông trên có phải là nút giao thông khác mức hay không?

Trả lời rút gọn:

a) Đường thẳng đi qua điểm và có vectơ chỉ phương là

Đường thẳng đi qua điểm và có vectơ chỉ phương là

Do ) nên hai đường thẳng và vuông góc với nhau

Do nên và chéo nhau

Vậy nút giao thông trên là nút giao thông khác mức

Bài 5.18: Trong không gian , một viên đạn được bắn ra từ điểm và trong 3 giây, đầu đạn đi với vận tốc không đổi; vectơ vận tốc (trên giây) là Hỏi viên đạn trên có bắn trúng mục tiêu trong mỗi tình huống sau hay không?

a) Mục tiêu đặt tại điểm

b) Mục tiêu đặt tại điểm

Trả lời rút gọn:

a) 

Do nên hai vecto và không cùng phương.

Vậy viên đạn trên không bắn trúng mục tiêu đặt tại điểm

b)

Do , tức nên hai vecto và cùng phương và ngược hướng.

Vậy viên đạn trên không bắn trúng mục tiêu đặt tại điểm

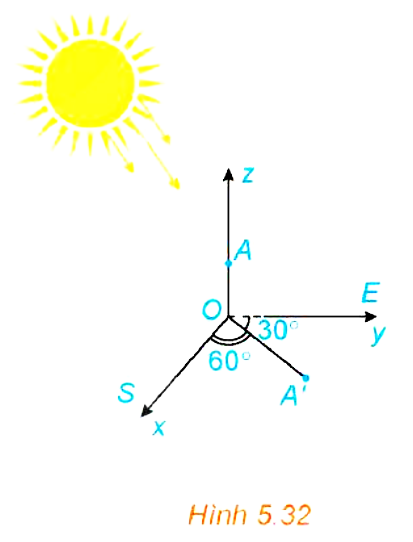
Bài 5.19: Trên mặt đất phẳng, người ta dựng một cây cột thẳng cao 6m vuông góc với mặt đất, có chân cột đặt tại vị trí trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột 3 m về hướng (hướng tạo với hướng nam góc và tạo với hướng đông góc ) (H.5.32). Chọn hệ trục có gốc toạ độ là , tia chỉ hướng nam, tia chỉ hướng đông, tia chứa cây cột, đơn vị đo là mét. Hãy viết phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét.

Trả lời rút gọn:

và

Đường thẳng đi qua và có vectơ chỉ phương nên có: 

• Phương trình tham số:
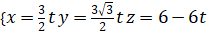
• Phương trình chính tắc: