Slide bài giảng Toán 12 kết nối Bài 16: Công thức tính góc trong không gian

Tóm lược nội dung

BÀI 16. CÔNG THỨC TÍNH GÓC TRONG KHÔNG GIAN

1. Công thức tính góc giữa hai đường thẳng

Hoạt động 1. Tìm mối quan hệ của góc giữa hai đường thẳng và góc giữa hai vecto chỉ phương

Trong không gian , cho hai đường thẳng và tương ứng có các vectơ chỉ phương (H5.34).

a) Hãy tìm mối quan hệ giữa các góc ; và

b) Có nhận xét gì về mối quan hệ giữa ; và ?

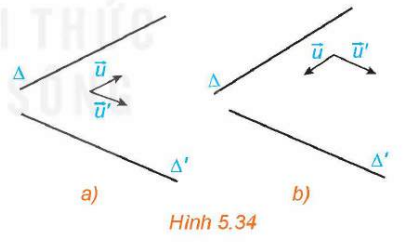
Trả lời rút gọn:

a)  Hai đường thẳng và tương ứng có các vectơ chỉ phương là nên giá của song song với và giá của song song với

H5.34a: ;

H5.34b: ;

b)

=> ; =

Luyện tập 1.Trong không gian , tính góc giữa trục và đường thẳng .

Trả lời rút gọn:

Trục và đường thẳng tương ứng có các vectơ chỉ phương là .

=>

2. Công thức tính góc giữa đường thẳng và mặt phẳng

Hoạt động 2. Tìm mối quan hệ giữa đường thẳng và mặt phẳng với góc giữa vectơ chỉ phương và vecto pháp tuyến tương ứng

Trong không gian , cho đường thẳng và mặt phẳng . Xét là một vecto chỉ phương của và (với giá ) là một vectơ pháp tuyến của (H5.35)

a) Hãy tìm mối quan hệ giữa các góc ; và

b) Có nhận xét gì về quan hệ giữa ; và ?

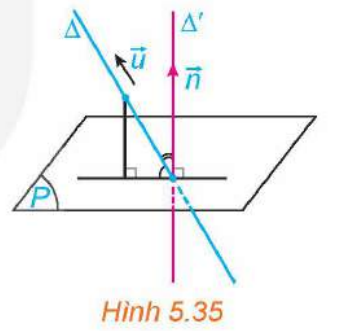
Trả lời rút gọn:

a) Mối quan hệ giữa các góc ; và ;

b) 

=> ; =

Luyện tập 2. Trong không gian , tính góc giữa đường thẳng và mặt phẳng với:

Trả lời rút gọn:

Đường thẳng có vecto chỉ phương là và mặt phẳng (P) có vecto pháp tuyến

Khi đó:

Vậy đường thẳng tạo với mặt phẳng góc

3. Công thức tính góc giữa hai mặt phẳng

Hoạt động 3. Tìm mối quan hệ của góc giữa hai mặt phẳng và góc giữa vecto pháp tuyến 

Trong không gian , cho hai mặt phẳng tương ứng có các vecto pháp tuyến là . Lấy các đường thẳng tương ứng các vectơ chỉ phương . (H5.36)

a) Góc giữa hai mặt phẳng và góc giữa hai đường thẳng có mối quan hệ gì?

b) Tính góc giữa hai mặt phẳng .

Trả lời rút gọn:

a) Do các đường thẳng tương ứng các vectơ chỉ phương nên đường thẳng vuông góc với mặt phẳng và đường thẳng vuông góc với mặt phẳng

=>  

b) ; =

=>

Luyện tập 3. Trong không gian , tính góc giữa hai mặt phẳng:

và  

Trả lời rút gọn:

Các mặt phẳng và tương ứng có các vectơ pháp tuyến là .

=> 

Vận dụng. Hãy trả lời câu hỏi đã được nêu ra trong tình huống mở đầu.

Một mái nhà hình tròn được đặt trên ba cây cột trụ (H.5.33). Các cây cột vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là 7m, 6m, 5m. Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 4m. Hỏi mái nhà nghiêng với mặt sàn nhà một góc bao nhiêu độ?

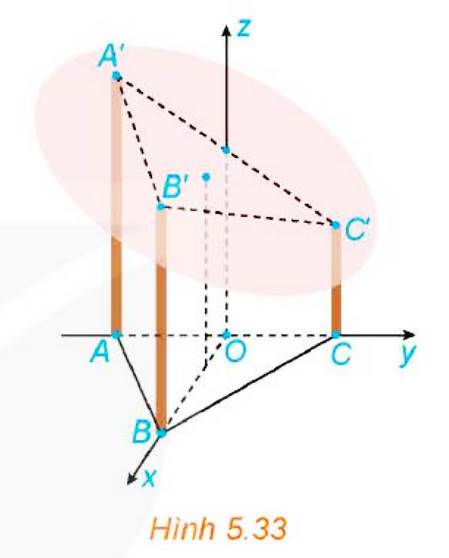
Trả lời rút gọn:

Mặt phẳng có hai vecto chỉ phương nên có vecto pháp tuyến .

  cũng là vectơ pháp tuyến của

Mặt phẳng có hai vecto chỉ phươngnên có vecto pháp tuyến . 

cũng là vectơ pháp tuyến của

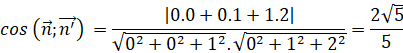
Vậy mái nhà nghiêng với mặt sàn nhà một góc .

GIẢI BÀI TẬP

Bài 5.20: Trong không gian , tính góc giữa hai đường thẳng:

và

Trả lời rút gọn:

Hai đường thẳng tương ứng có các vectơ chỉ phương là .

=>

Bài 5.21: Trong không gian , tính góc giữa trục và mặt phẳng

Trả lời rút gọn:

Trục có vecto chỉ phương là và mặt phẳng (P) có vecto pháp tuyến

Vậy trục tạo với mặt phẳng góc

Bài 5.22: Tính góc giữa đường thẳng và mặt phẳng

Trả lời rút gọn:

Đường thẳng có  và mặt phẳng (P) có

Vậy đường thẳng tạo với mặt phẳng góc

Bài 5.23: Kim tự tháp Kheops ở Ai Cập có dạng hình chóp , có đáy là hình vuông với cạnh dài 230m, các cạnh bên bằng nhau và dài 219m (theo britannica.com) (H.5.38). Tính góc giữa hai mặt phẳng và

Trả lời rút gọn: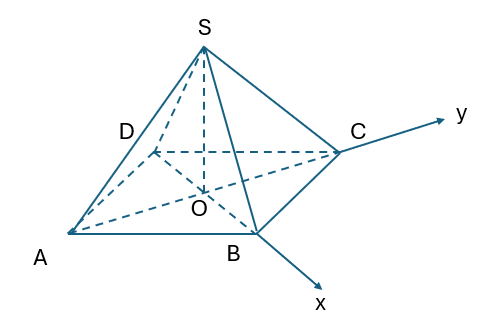

Do là hình vuông nên  

Mặt phẳng nhận và làm cặp vectơ chỉ phương nên có vecto pháp tuyến là:

Mặt phẳng nhận và làm cặp vectơ chỉ phương nên có vecto pháp tuyến là:

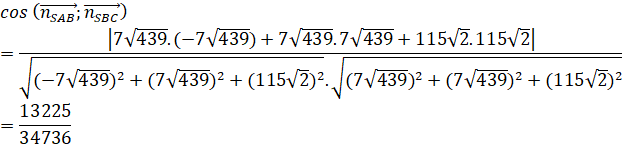
Vậy góc giữa hai mặt phẳng là .

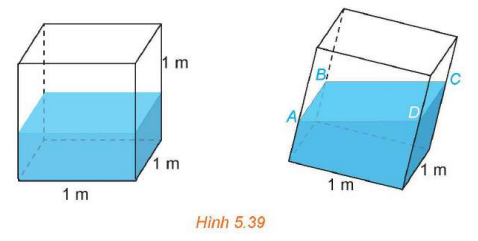
Bài 5.24: (H.5.39) Trong một bể hình lập phương cạnh 1m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành và khoảng cách từ các điểm đến đáy bể tương ứng là 40cm, 44cm, 48cm.

a) Khoảng cách từ điểm đến đáy bể bằng bao nhiêu centimét? (Tính gần đúng, lấy giá trị nguyên.)

b) Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?

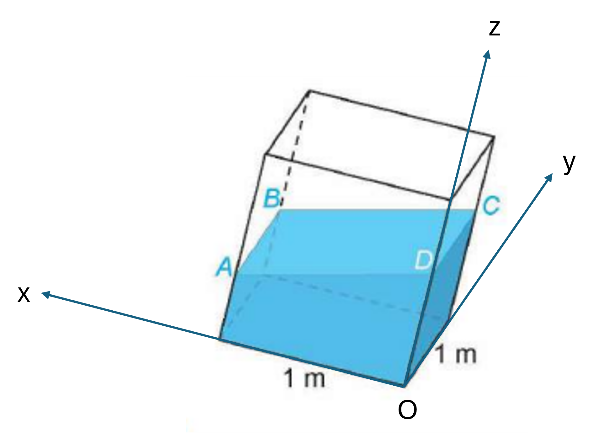
Trả lời rút gọn:

a) Kẻ hệ trục toạ độ Oxyz như hình bên.

ABCD là hình bình hành nên  

Vậy khoảng cách từ điểm D đến đáy bể bằng .

b)

Mặt phẳng có hai vecto chỉ phương nên có vecto pháp tuyến .

  cũng là vectơ pháp tuyến của

Mặt phẳng có hai vecto chỉ phương nên có vecto pháp tuyến . 

Vậy đáy bể nghiêng so với mặt phẳng nằm ngang một góc .