Slide bài giảng Toán 12 kết nối Bài tập cuối chương III
Slide điện tử Bài tập cuối chương III. Kiến thức bài học được hình ảnh hóa, sinh động hóa. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 12 Kết nối tri thức sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI TẬP CUỐI CHƯƠNG III
A. TRẮC NGHIỆM
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:
| Tuổi thọ |
|
|
|
|
|
| Số con hổ | 1 | 3 | 8 | 6 | 2 |
Giải rút gọn bài 3.9 trang 85 sách toán 12 tập 1 kntt
Khoảng biến thiên của mẫu số liệu ghép nhóm này là:
- 3.
- 4.
- 5.
- 6.
Giải rút gọn:
Chọn đáp án C.
Giải rút gọn bài 3.10 trang 85 sách toán 12 tập 1 kntt
Nhóm chứa tứ phân vị thứ nhất là:
 .
.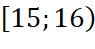 .
. .
. 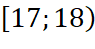 .
.
Giải rút gọn:
Chọn đáp án C.
Giải rút gọn bài 3.11 trang 85 sách toán 12 tập 1 kntt
Nhóm chứa tứ phân vị thứ ba là:
 .
. .
. .
. 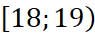 .
.
Giải rút gọn:
Chọn đáp án C.
Giải rút gọn bài 3.12 trang 85 sách toán 12 tập 1 kntt
Số đặc trưng nào không sử dụng thông tin của nhóm số liệu đầu tiên và nhóm số liệu cuối cùng?
- Khoảng biến thiên.
- Khoảng tứ phân vị.
- Phương sai.
- Độ lệch chuẩn.
Giải rút gọn:
Chọn đáp án B.
Giải rút gọn bài 3.13 trang 85 sách toán 12 tập 1 kntt
Nếu thay tất cả các tần số trong mẫu số liệu ghép nhóm trên bằng 4 thì số đặc trưng nào sau đây không thay đổi?
- Khoảng biến thiên.
- Khoảng tứ phân vị.
- Phương sai.
- Độ lệch chuẩn.
Giải rút gọn:
Chọn đáp án A.
B. TỰ LUẬN
Giải rút gọn bài 3.14 trang 86 sách toán 12 tập 1 kntt
Để đánh giá chất lượng một loại pin điện thoại mới, người ta ghi lại thời gian nghe nhạc liên tục của điện thoại được sạc đầy pin cho đến khi hết pin cho kết quả như sau:
| Thời gian (giờ) |
|
|
|
|
|
| Số chiếc điện thoại (tần số) | 2 | 8 | 15 | 10 | 5 |
Tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Giải rút gọn:
Khoảng biến thiên:![]()
Cỡ mẫu:![]()
Tứ phân vị thứ nhất của mẫu số liệu là  , vì
, vì ![]() ,
, ![]() nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là
nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là ![]() .
.
Tứ phân vị thứ ba của mẫu số liệu là 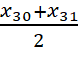 , thuộc nhóm
, thuộc nhóm ![]() nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là
nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là 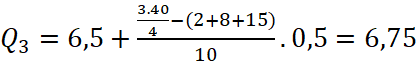 .
.
Khoảng biến thiên: ![]() .
.
Chọn giá trị đại diện cho các nhóm số liệu, ta có:
| Thời gian (giờ) |
|
|
|
|
|
| Giá trị đại diện | 5,25 | 5,75 | 6,25 | 6,75 | 7,25 |
| Số chiếc điện thoại (tần số) | 2 | 8 | 15 | 10 | 5 |
Thời gian trung bình nghe nhạc liên tục của điện thoại là:![]()
Phương sai của mẫu số liệu:
Độ lệch chuẩn của mẫu số liệu:![]()
Giải rút gọn bài 3.15 trang 86 sách toán 12 tập 1 kntt
Người ta ghi lại tiền lãi (đơn vị: triệu đồng) của một số nhà đầu tư (với số tiền đầu tư như nhau), khi đầu tư vào hai lĩnh vực A, B cho kết quả như sau:
| Tiền lãi |
|
|
|
|
|
| Số nhà đầu tư vào lĩnh vực A | 2 | 5 | 8 | 6 | 4 |
| Số nhà đầu tư vào lĩnh vực B | 8 | 4 | 2 | 5 | 6 |
- Về trung bình, đầu tư vào lĩnh vực nào đem lại tiền lãi cao hơn?
- Tính độ lệch chuẩn cho các mẫu số liệu về tiền lãi của các nhà đầu tư ở hai lĩnh vực này và giải thích ý nghĩa của các số thu được.
Giải rút gọn:
- Ta có mẫu số liệu ghép nhóm với giá trị đại diện là:
| Tiền lãi |
|
|
|
|
|
| Giá trị đại diện | 7,5 | 12,5 | 17,5 | 22,5 | 27,5 |
| Số nhà đầu tư vào lĩnh vực A | 2 | 5 | 8 | 6 | 4 |
| Số nhà đầu tư vào lĩnh vực B | 8 | 4 | 2 | 5 | 6 |
Tiền lãi trung bình khi đầu tư vào lĩnh vực A là: ![]() (triệu đồng)
(triệu đồng)
Tiền lãi trung bình khi đầu tư vào lĩnh vực B là: ![]() (triệu đồng)
(triệu đồng)
Như vậy, về trung bình, đầu tư vào lĩnh vực A đem lại tiền lãi cao hơn.
- Khi đầu tư vào lĩnh vực A:
Phương sai:  ; độ lệch chuẩn:
; độ lệch chuẩn:  (triệu đồng)
(triệu đồng)
Khi đầu tư vào lĩnh vực A:
Phương sai:  ; độ lệch chuẩn:
; độ lệch chuẩn:  (triệu đồng)
(triệu đồng)
Như vậy, độ lệch chuẩn của mẫu số liệu về tiền lãi đầu tư vào lĩnh vực B lớn hơn độ lệch chuẩn của mẫu số liệu về tiền lãi đầu tư vào lĩnh vực A nên đầu tư vào lĩnh vực B là rủi ro hơn.
Giải rút gọn bài 3.16 trang 86 sách toán 12 tập 1 kntt
Thành tích môn nhảy cao của các vận động viên tại một giải điền kinh dành cho học sinh trung học phổ thông như sau:
| Mức xà (cm) |
|
|
|
|
| Số vận động viên | 3 | 10 | 6 | 1 |
- Tính các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm trên.
- Độ phân tán của mẫu số liệu cho biết điều gì?
Giải rút gọn:
- Khoảng biến thiên của mẫu số liệu:

Cỡ mẫu:![]()
Vì 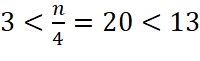 nên nhóm
nên nhóm ![]() chứa tứ phân vị thứ nhất.
chứa tứ phân vị thứ nhất.
Do đó tứ phân vị thứ nhất là:
Vì 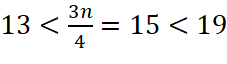 nên nhóm
nên nhóm ![]() chứa tứ phân vị thứ ba.
chứa tứ phân vị thứ ba.
Do đó tứ phân vị thứ ba là:
Khoảng tứ phân vị là: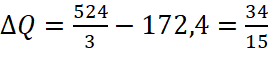
Mẫu số liệu với giá trị đại diện:
| Mức xà (cm) |
|
|
|
|
| Giá trị đại diện | 171 | 173 | 175 | 177 |
| Số vận động viên | 3 | 10 | 6 | 1 |
Giá trị trung bình: ![]() (cm)
(cm)
Phương sai của mẫu số liệu:
Độ lệch chuẩn của mẫu số liệu:![]() (cm)
(cm)
- Độ phân tán của mẫu số liệu cho biết:
- Độ biến thiên của mẫu số liệu gốc xấp xỉ
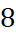 cm.
cm. - Khoảng tứ phân vị của mẫu số liệu gốc xấp xỉ
 cm
cm - Phương sai của mẫu số liệu gốc xấp xỉ

- Độ lệch chuẩn của mẫu số liệu gốc xấp xỉ
 (cm).
(cm).
Giải rút gọn bài 3.17 trang 86 sách toán 12 tập 1 kntt
Trong bài thực hành đo hiệu điện thế của mạch điện, An và Bình đã dùng hai vôn kế khác nhau để đo, mỗi bạn tiến hành đo 10 lần cho kết quả như sau:
| Hiệu điện thế đo được (Vôn) |
|
|
|
|
| Số lần An đo | 1 | 6 | 2 | 1 |
| Số lần Bình đo | 1 | 3 | 4 | 2 |
Tính độ lệch chuẩn của các mẫu số liệu ghép nhóm cho kết quả đo của An và Bình. Từ đó kết luận xem vôn kế của bạn nào cho kết quả đo ổn định hơn.
Giải rút gọn:
Mẫu số liệu với giá trị đại diện
| Hiệu điện thế đo được (Vôn) |
|
|
|
|
| Giá trị đại diện | 3,875 | 3,925 | 3,975 | 4,025 |
| Số lần An đo | 1 | 6 | 2 | 1 |
| Số lần Bình đo | 1 | 3 | 4 | 2 |
Xét kết quả đo của An:
Giá trị trung bình: ![]() ;
;
Phương sai: 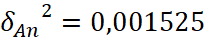 ; độ lệch chuẩn:
; độ lệch chuẩn:![]()
Xét kết quả đo của Bình:
Giá trị trung bình: ![]() ;
;
Phương sai:  ; độ lệch chuẩn:
; độ lệch chuẩn:![]()
Vì ![]() nên Vôn kế của bạn An cho kết quả ổn định hơn.
nên Vôn kế của bạn An cho kết quả ổn định hơn.
