Slide bài giảng Toán 12 kết nối Bài tập cuối chương VI

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG VI

A. TRẮC NGHIỆM

Sử dụng dữ kiện sau để trả lời các câu hỏi từ 6.12 đến 6.14

Cho .

Bài 6.12: Giá trị của là:

A.                      B.                      C.                       D.

Giải chi tiết:

A.  

Bài 6.13: Giá trị của là:

A.                       B.                      C.                      D.

Trả lời rút gọn:

D.

Bài 6.14: Giá trị của là:

A.                      B.                      C.                      D.

Trả lời rút gọn:

B.

Sử dụng dữ kiện sau để trả lời các câu từ 6.15 đến 6.17

Bạn An có một túi gồm một số chiếc kẹo cùng loại, chỉ khác màu, trong đó có 6 chiếc kẹo sô cô la đen, còn lại 4 chiếc kẹo sô cô la trắng. An lấy ngẫu nhiên 1 chiếc kẹo trong túi để cho Bình, rồi lại lấy ngẫu nhiên tiếp 1 chiếc kẹo nữa trong túi và cũng đưa cho Bình.

Bài 6.15: Xác suất để Bình nhận được 2 chiếc kẹo sô cô la đen là

A.                       B.                       C.                       D.

Trả lời rút gọn:

A.

A là biến cố:”An lấy chiếc kẹo sô cô la đen ở lần thứ nhất”

B là biến cố:”An lấy chiếc kẹo sô cô la đen ở lần thứ hai”

Ta có ban đầu trong túi có 6 chiếc kẹo sô cô la đen nên:

Nếu A đã xảy ra tức trong túi còn lại 9 chiếc kẹo với 5 chiếc kẹo sô cô la đen và 4 chiếc kẹo sô cô la trắng

Bài 6.16: Xác suất để Bình nhận được 2 chiếc kẹo sô cô la trắng là

A.                       B.                      C.                      D.

Trả lời rút gọn:

B.

A là biến cố:”An lấy chiếc kẹo sô cô la trắng ở lần thứ nhất”

B là biến cố:”An lấy chiếc kẹo sô cô la trắng ở lần thứ hai”

Ta có ban đầu trong túi có 4 chiếc kẹo sô cô la đen nên:

Nếu A đã xảy ra tức trong túi còn lại 9 chiếc kẹo với 6 chiếc kẹo sô cô la đen và 3 chiếc kẹo sô cô la trắng

Bài 6.17: Xác suất để Bình nhận được chiếc kẹo sô cô la đen ở lần thứ nhất, chiếc kẹo sô cô la trắng ở lần thứ hai là

A.                       B.                      C.                       D.

Trả lời rút gọn:

Không có đáp án

 A là biến cố:”An lấy chiếc kẹo sô cô la đen ở lần thứ nhất”

B là biến cố:”An lấy chiếc kẹo sô cô la trắng ở lần thứ hai”

Ta có ban đầu trong túi có 6 chiếc kẹo sô cô la đen nên:

Nếu A đã xảy ra tức trong túi còn lại 9 chiếc kẹo với 5 chiếc kẹo sô cô la đen và 4 chiếc kẹo sô cô la trắng

B. TỰ LUẬN

Bài 6.18: Để thử nghiệm tác dụng điều trị bệnh mất ngủ của hai loại thuốc X và thuốc Y, người ta tiến thành thử nghiệm trên 4000 người bệnh tình nguyện. Kết quả được cho trong bảng thống kê 2 × 2 sau:

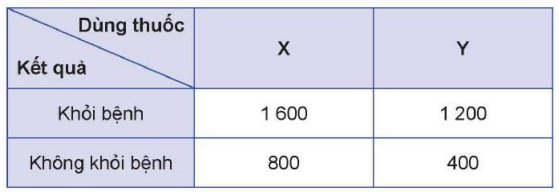
Chọn ngẫu nhiên 1 người bệnh tham gia tình nguyện thử nghiệm thuốc.

a) Tính xác suất để người đó khỏi bệnh nếu biết người bệnh đó uống thuốc X.

b) Tính xác suất để người bệnh đó uống thuốc Y, biết rằng người đó khỏi bệnh.

Trả lời rút gọn:

a) A là biến cố:”Người đó uống thuốc X”; B là biến cố:”Người đó khỏi bệnh”

AB là biến cố:”Người đó uống thuốc X và khỏi bệnh”

Số người uống thuốc X là 1600 + 800 = 2400 ⇒

Trong số những người uống thuốc X, có 1600 người khỏi bệnh

⇒

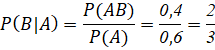
b) A là biến cố:”Người đó uống thuốc Y”; B là biến cố:”Người đó khỏi bệnh”

AB là biến cố:”Người đó uống thuốc Y và khỏi bệnh”

Số người khỏi bệnh là 1600 + 1200 = 2800 ⇒

Trong số những người khỏi bệnh, có 1200 người uống thuốc Y 

⇒

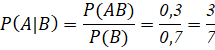
Bài 6.19: Một nhóm có 25 học sinh, trong đó có 14 em học khá môn Toán, 16 em học khá môn Vật lý, 1 em không học khá cả hai môn Toán và môn Vật lý. Chọn ngẫu nhiên một học sinh trong số đó. Tính xác suất để học sinh đó:

a) Học khá môn Toán, đồng thời học khá môn Vật lý,

b) Học khá môn Toán, nhưng không học khá môn Vật lý;

c) Học khá môn Toán, biết rằng học sinh đó học khá môn Vật lý.

Trả lời rút gọn:

A là biến cố:”Học sinh học khá môn Toán”

B là biến cố:”Học sinh học khá môn Lý”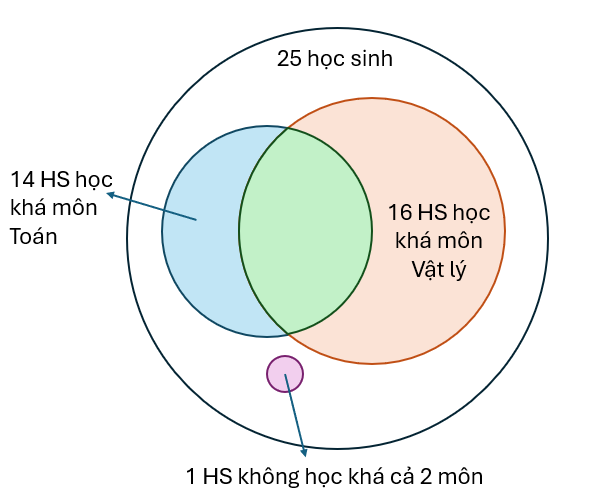

a) AB là biến cố:”Học sinh học khá môn Toán, đồng thời học khá môn Vật lý”

Số học sinh học khá môn Toán, đồng thời học khá môn Vật lý là:

Vậy xác suất để học sinh đó học khá môn Toán, đồng thời học khá môn Vật lý là

b) Số học sinh học khá môn Toán, nhưng không học khá môn Vật lý là:

Vậy xác suất để học sinh đó học khá môn Toán, nhưng không học khá môn Vật lý là

c) 

Có 16 em học khá môn Vật lý nên xác suất để học sinh đó học khá môn Vật lý là:

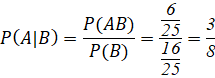
Vậy xác suất để học sinh đó học khá môn Toán, biết rằng học sinh đó học khá môn Vật lý là

Bài 6.20: Chuồng I có 5 con gà mái, 2 con gà trống. Chuồng II có 3 con gà mái, 5 con gà trống. Bác Mai bắt một con gà trong số đó theo cách sau: “Bác tung một con xúc xắc cân đối, đồng chất. Nếu số chấm chia hết cho 3 thì bác chọn chuồng I. Nếu số chấm không chia hết cho 3 thì bác chọn chuồng II. Sau đó, từ chuồng đã chọn bác bắt ngẫu nhiên một con gà”. Tính xác suất để bác Mai bắt được con gà mái.

Trả lời rút gọn:

A là biến cố:”Số chấm chia hết cho 3”

B là biến cố:”Con gà bắt được là con gà mái”

Các kết quả thuận lợi cho biến cố A là: 3, 6

Khi A xảy ra tức bác Mai bắt gà ở chuồng I với 5 con gà mái và 2 con gà trống nên xác suất để bác Mai bắt được con gà mái ở chuồng I là:

Khi A không xảy ra tức bác Mai bắt gà ở chuồng II với 3 con gà mái và 5 con gà trống nên xác suất để bác Mai bắt được con gà mái ở chuồng II là:

Vậy xác suất để bác Mai bắt được con gà mái là

Bài 6.21: Một loại vaccine được tiêm ở địa phương X. Người có bệnh nền thì với xác suất 0,35 có phản ứng phụ sau tiêm; người không có bệnh nền thì chỉ có phản ứng phụ sau tiêm với xác suất 0,16. Chọn ngẫu nhiên một người được tiêm vaccine và người này có phản ứng phụ. Tính xác suất để người này có bệnh nền, biết rằng tỉ lệ người có bệnh nền ở địa phương X là 18%.

Trả lời rút gọn:

A là biến cố:”Người đó bị bệnh nền”

B là biến cố:”Người đó có phản ứng phụ sau tiêm vaccine”

Ta có tỉ lệ người có bệnh nền ở địa phương X là 18% nên

Người có bệnh nền thì với xác suất 0,35 có phản ứng phụ sau tiêm nên

Người không có bệnh nền thì chỉ có phản ứng phụ sau tiêm với xác suất 0,16 nên

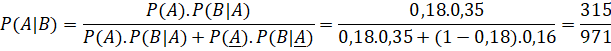
Vậy xác suất để người này có bệnh nền khi chọn ngẫu nhiên một người được tiêm vaccine và người này có phản ứng phụ là